How do you tell whether the graph opens up or down, find the vertex, and find the axis of symmetry of #y=2(x-1)^2-6#?
2 Answers
Vertex is
Axis of symmetry
Explanation:
Given -
#y=2(x-1)^2-6#
It is like -
#y=a(x-h)+k#
Where#(h, k)# is the vertex.
Since it is in terms of#y# it is either facing up or down.
If#a# is positive, the parabola is facing up.
If#a# is negative, the parabola is facing down.
Axis of symmetry is#x=h#
#h=-(-1)=1#
#k=+(-6)=-6#
Vertex is
Axis of symmetry
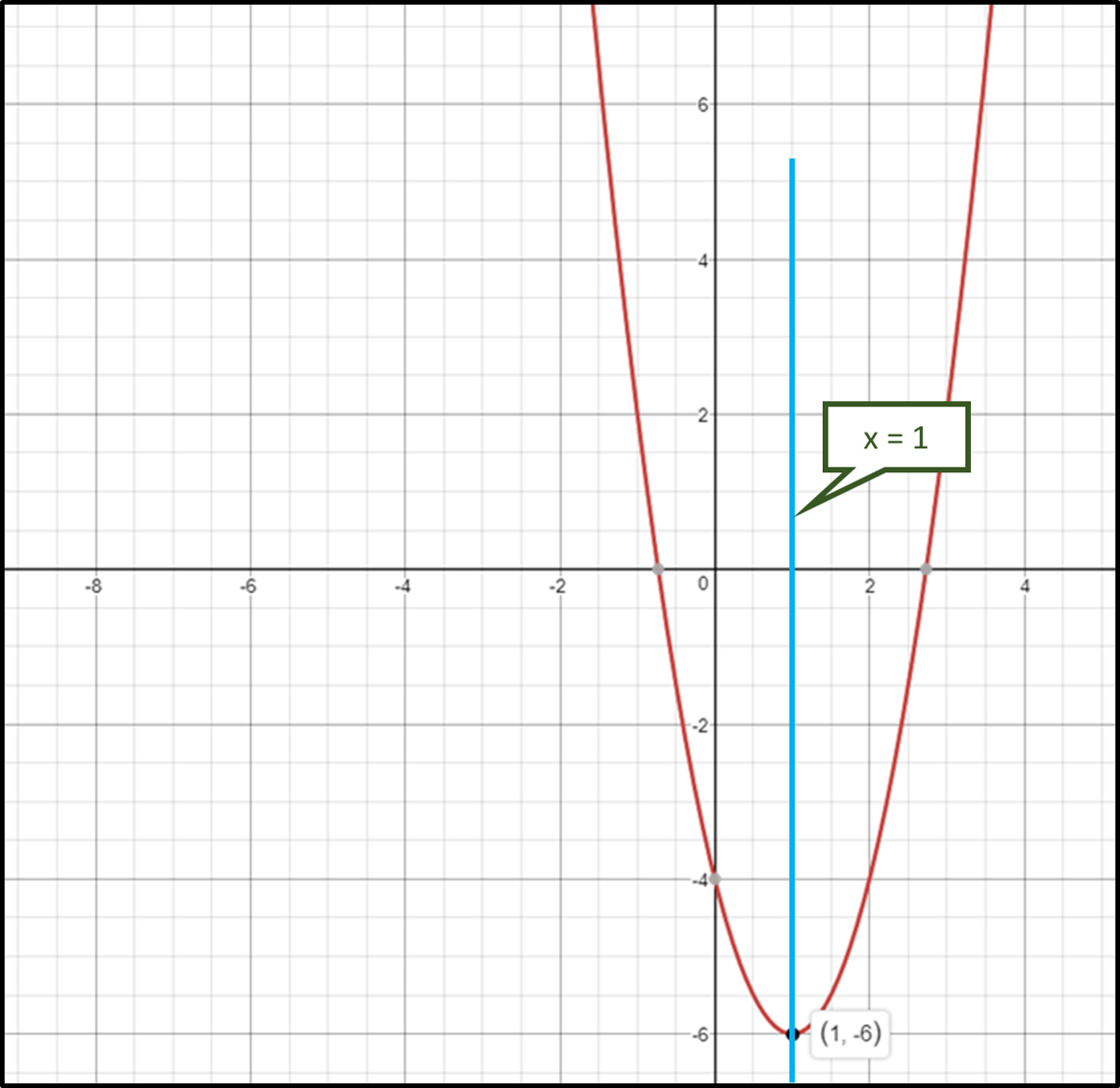
Axis of symmetry is
Explanation:
The given equation is in vertex form i.e.
In the equation
Axis of symmetry is
graph{(x-1)(y-2(x-1)^2+6)((x-1)^2+(y+6)^2-0.04)=0 [-20, 20, -10, 10]}

