Find the values of #c# such that the area...?
Find the values of #c# such that the area of the region bounded by the parabolas #y=x^2-c^2# and #y=c^2-x^2# is 576.
Find the values of
1 Answer
Sep 19, 2017
Explanation:
The two curves are:
and
We can note that for every
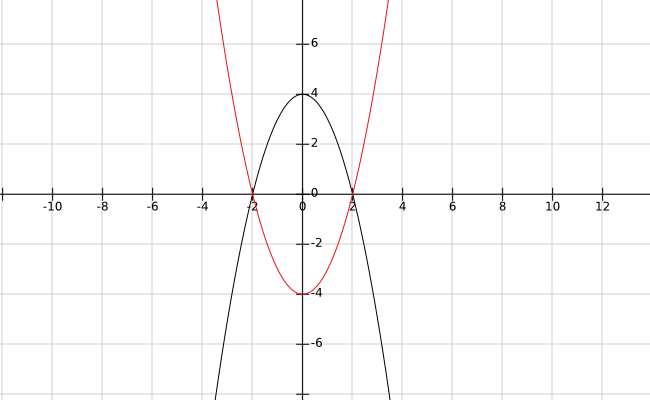
Given the symmetry, the area bounded by the two parabolas is twice the area bounded by either parabola and the
If we choose
and posing
we get:

