Let us consider the isosceles trapezoid #ABCD#, where #BC#||#AD# and #AB=CD# as shown below, in which we have drawn #CE#||#AB#.
As #CE#||#AB#, we have #m/_BAE=m/_CED#
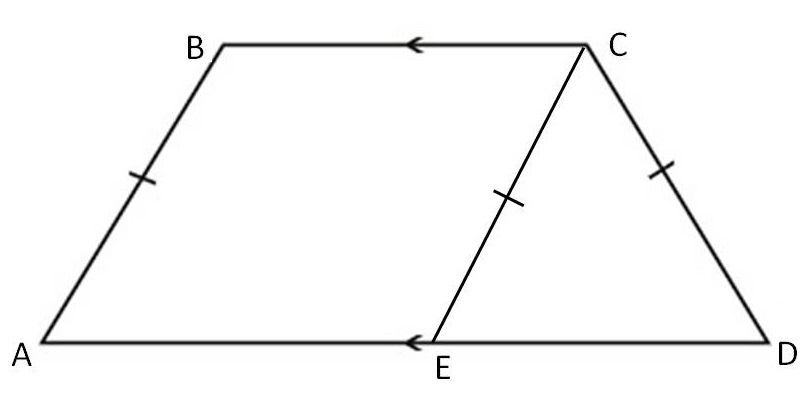
As #AB#||#CE# and #AE#||#BC#, #ABCE# is a parallelogram and hence #AB=CE# and , but as #AB=CD#, we have #CD=CE#.
Therefore #DeltaCDE# is an isosceles triangle and hence #m/_CED=m/_CDE#.
But as #m/_BAE=m/_CED#, we have #m/_BAE=m/_CDE# or #m/_BAD=m/_ADC#
Further as #AD#||#BC#, #/_ABC# is supplementary to #/_BAD# and similarly #/_ADC# and #/_BCD# are supplementary.
As #/_ABC# and #/_BCD# are supplementary of equal angles, they too are equal.
#Q.E.D.#
Note #-# I have not used #E# as a midpoint of #AD#.

