Question

What are the vertex, focus and directrix of `y=(x-1)^2-1`?

Answer 1

Vertex `(1,-1)`

Focus `(1, -0.75)`
Directrix `y=-1.25`

Explanation:

Given -

`y=(x-1)^2-1`

We have to find the vertex, focus and directrix.

The given equation is in the form.

`y=a(x-h)^2+k`

It is in the vertex form. Then its vertex is `(h, k)`

Obtain the values of `h` and `k` from the given equation.

`h= 1` x-coordinate of the vertex
`k=-1` y coordinate of the vertex

Then the vertex of the given equation is `(1, -1)`

If the term `a` in the equation `y=a(x-h)^2+k` is positive, it means the curve opens up.

In the given equation `a=1`. one is a positive value, hence the parabola of the given equation opens up.

The standard form of a parabola of this type is as follows.
[for a parabola whose vertex is away from origin]

`(x-h)^2=4a(y-k)`

Where

4 is a constant

`a` is the distance between vertex and focus.

We shall rewrite the given equation like this

`y=(x-1)^2-1`

`(x-1)^2-1=y`

`(x-1)^2=y+1`

It can be written as

`(x-1)^2=(y+1)`

It appears, there is no `4a` term.We shall bring it like this.

`(x-1)^2=(y+1)` this equation can be written like this

`(x-1)^2=1 xx (y+1)`

One is equal to `4 xx 1/4`

So we can replace one with `4 xx 1/4` and rewrite

`(x-1)^2=4 xx1/4xx (y+1)`

Now we have the constant term 4. `1/4` is `a`

The distance between vertex and focus or vertex and directrix is `a=1/4`

We can find the focus and directrix.

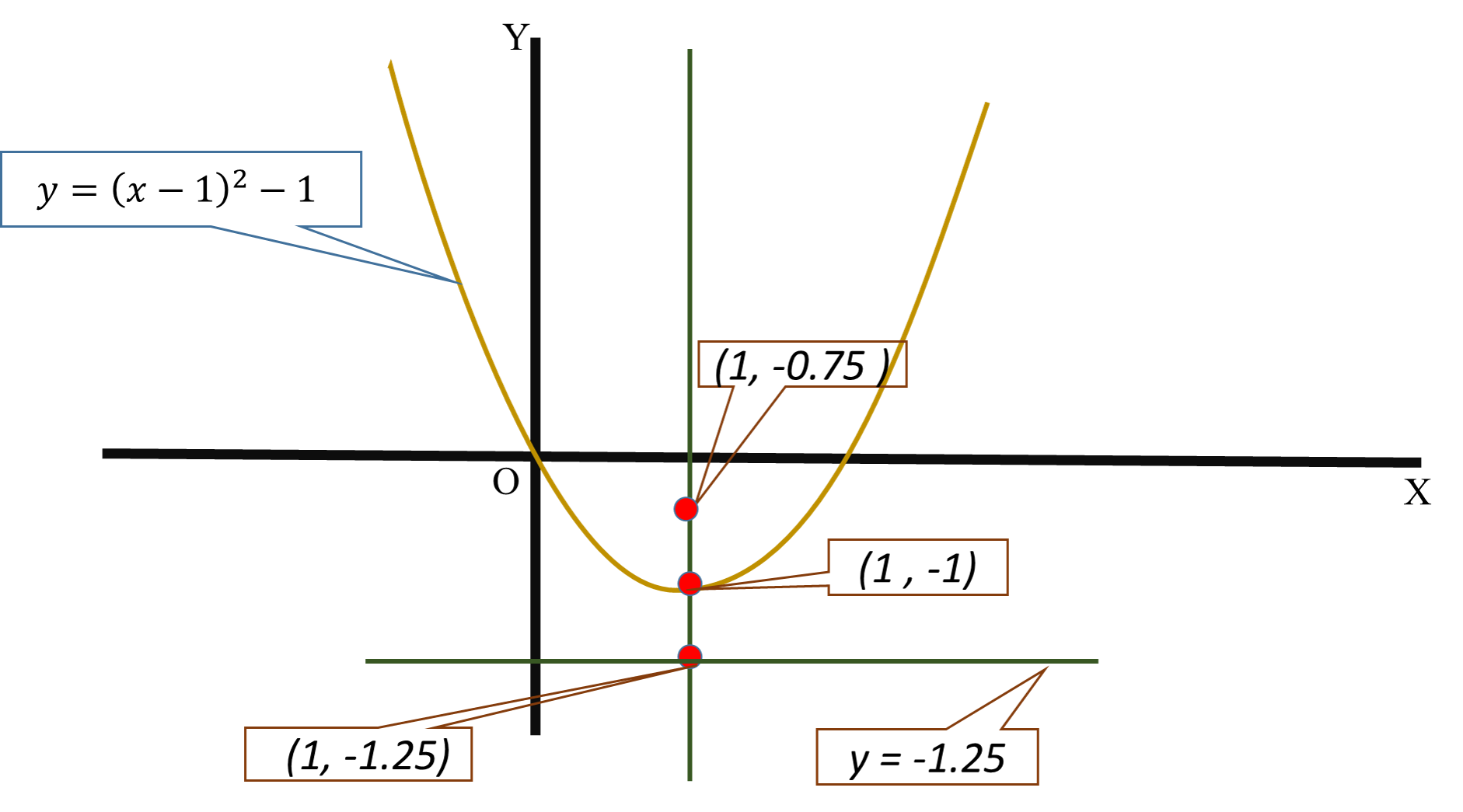
The point which lies vertically at a distance of 0.25 above vertex is focus.

Focus is `(1, (-1+0.25))`; `(1, -0.75)`

Find the point the lies vertically at a distance of 0.25 below vertex.
Use its y- coordinate to find the equation of directrix.

`(1, (-1 + (-25)))`
`(1, (-1 -25))`
`(1, -1.25)`

Directrix `y=-1.25`