Two corners of a triangle have angles of # (2 pi )/ 3 # and # ( pi ) / 4 #. If one side of the triangle has a length of # 15 #, what is the longest possible perimeter of the triangle?
2 Answers
Explanation:
By observation, the longest length would be opposite the widest angle, and the shortest length opposite the smallest angle. The smallest angle, given the two stated, is
Using the length of 15 as the shortest side, the angles on each side of it are those given. We can calculate the triangle height
Now, the other sides are:
Thus, the maximum perimeter is:
Perimeter
Explanation:
let
therefore;
using angle sum property
Using the sine rule
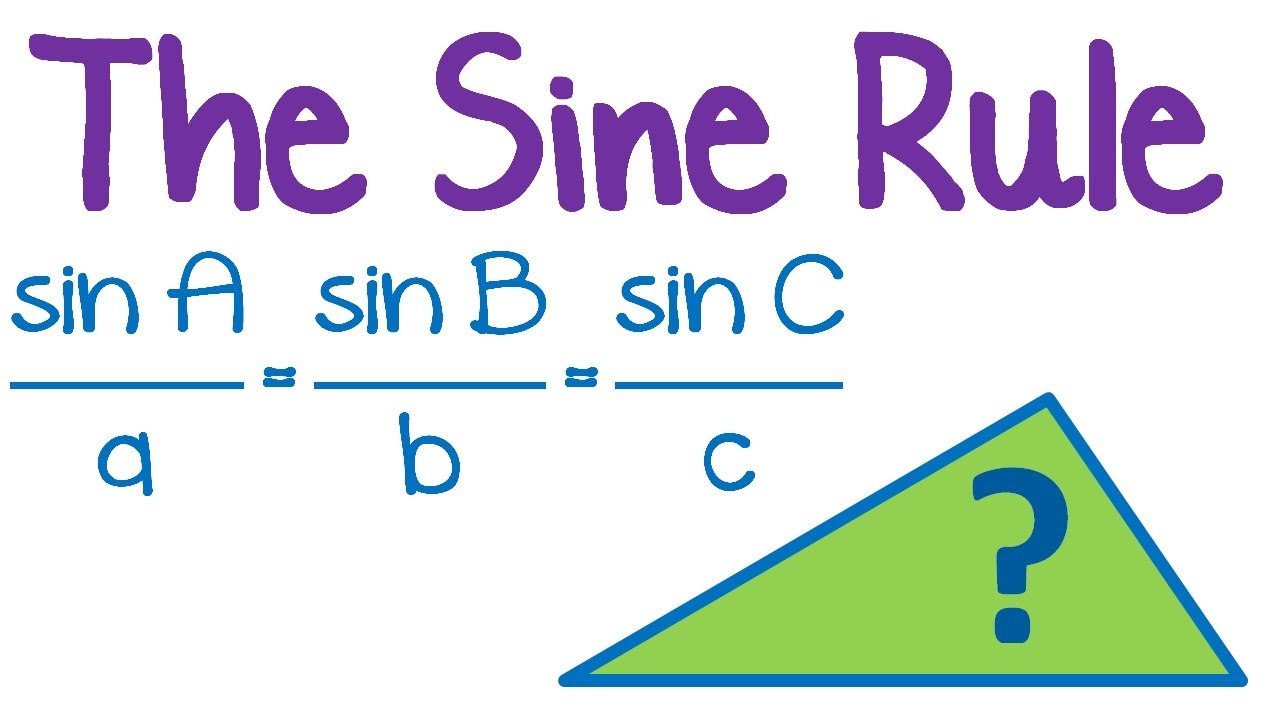
perimeter



