Two corners of an isosceles triangle are at #(1 ,3 )# and #(1 ,4 )#. If the triangle's area is #64 #, what are the lengths of the triangle's sides?
1 Answer
Lengths of sides:
Explanation:
The vertices at
So one side of the triangle has a length of
Note that the equal length sides of the isosceles triangle can not be both equal to
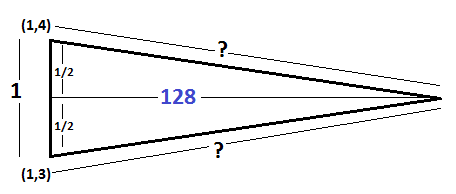
If we use the side with length
(Since
Bisecting the base to form two right triangles and applying the Pythagorean Theorem, the lengths of the unknown sides must be
(Notice that the height to base ratio is so great, there is no significant difference between the height and the length of the other side).
