Question

How do you solve the system of equations by graphing `x+y=3` and `x-y=1` and then classify the system?

Answer 1

This pair of equations are consistent with a single solution
`x=2`, `y=1`

Explanation:

Graphing solution (sorry I missed this requirement initially.
The graph of `x+y=3` looks like:
graph{(3-x) [-10, 10, -5, 5]}
and
the graph of `x-y=1` looks like
graph{x-1 [-12.66, 12.65, -6.33, 6.33]}

When combined we have

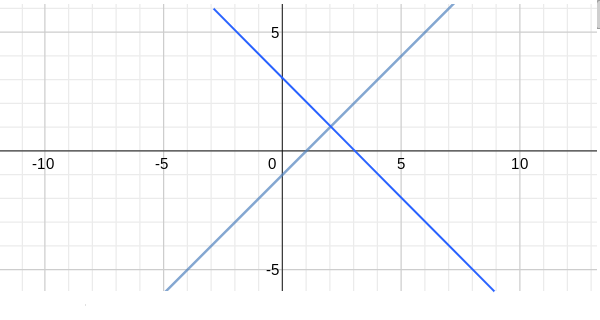
with a single point of intersection at `(x,y)=(2,1)`

Non-graphing solution
Given
[1]`color(white)("XXX")x+y=3`
[2]`color(white)("XXX")x-y=1`

adding [1] and [2] together gives
[3]`color(white)("XXX")2x=4`
which implies
[4]`color(white)("XXX")x=2`

subtracting [2] from [1] gives
[5]`color(white)("XXX")2y=2`
which implies
[6]`color(white)("XXX")y=1`

This pair of equations are consistent with a single solution
`x=2`, `y=1`