Question

A rectangle `OABC` is drawn so that `O` is the vertex of parabola `y=x^2` and `OA` and `OB` are two chords drawn on the parabola. What is the locus of point `C`?

(A). `y=x^2+2`
(B). `y=-x^2+4`
(C). `y=2x^2`
(D). `y=-2x^2+4`

Answer 1

(A) `y=x^2+2`

Explanation:

The parabola `y=x^2` is symmetric w.r.t. `y`-axis. Further as `OABC` is a rectangle, its each angle is `90^@` i.e. `m/_AOB=90^@`.

As the sides `AO` and `BO` pass through origin at `O(0,0)`, their equation will be will be of type `y=mx` and `y=-1/mx` or `x+my=0`.

Now intersection of `y=mx` with parabola will be given by `mx=x^2` i.e. `x=m` and the corresponding point is `(m,m^2)`. Similarly intersection of `x+my=0` gives `x+mx^2=0` i.e. `x=-1/m` and the corresponding point is `(-1/m,1/m^2)`.

As `A(m,m^2)` and `B(-1/m,1/m^2)`, we must have `C(m-1/m,m^2+1/m^2)` and as

`(m-1/m)^2=m^2+1/m^2-2`, desired equation is `y=x^2+2` and answer is (A).

Below is shown the graph and rectangle relating to `m=2`.

graph{(y-x^2)(2y+x)(y-2x)(8x-4y+5)(2x+4y-20)(y-x^2-2)=0 [-4.84, 5.16, -0.38, 4.62]}

Answer 2

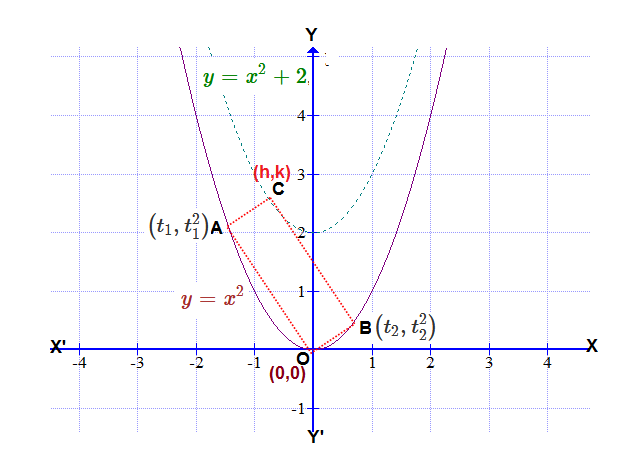
I think that name of the rectangle should be `OACB` not `OABC`

Let the coordinates of

A `->(t_1,t_1^2)`
B `->(t_2,t_2^2)`
C `->(h,k)`
O `->(0,0)`

Gradient of OA `=t_1^2/t_1=t_1`
Gradient of OB `=t_2^2/t_2=t_2`

As OA and OB are adjacent sides of the rectangle then product of their gradients should be `-1`
Hence #t_1*t_2=-1... .(1)#

Now the diagonals ºC and `AB` should bisect each other.
So coordinates of mid point of `OC->(h/2,k/2)`

And coordinates of mid point of `AB->((t_1+t_2)/2,(t_1^2+t_2^2)/2)`

Hence `h=t_1+t_2 and k=(t_1^2+t_2^2)`

So `k=(t_1^2+t_2^2)`
`=>k=(t_1+t_2)^2-2t_1t_2`
`=>k=h^2-2(-1)`
`=>k=h^2+2`

Converting `(h,k)->(x,y)` we get the locus of `C` as follows

`color(green)(y=x^2+2`, which is option `(A)`