Question

What is the orthocenter of a triangle with corners at `(4 ,1 )`, `(6 ,2 )`, and (3 ,6 )#?

Answer 1

Coordinates of Orthocenter `color(blue)(O (56/11, 20/11))`

Explanation:

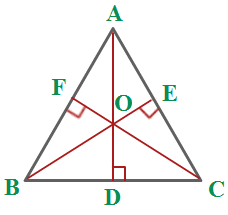
Orthocenter is the concurring point of the three altitudes of a triangle and represented by ‘O’

Slope of BC `= m_a = (6-2) / (3-6) = -(4/3)`

`Slope of AD = -(1/m_a) = (3/4)`

Equation of AD is

`y - 1 = (3/4) (x - 4)`

`4y - 3x = -8` Eqn (1)

Slope of AB `= m_c = (2 - 1) / 6-4) = (1/2)`

Slope of CF = -(1/m_c) = -2#

Equation of CF is

`y - 6 = -2 (x - 3)`

`y + 2x = 12` Eqn (2)

Solving Eqns (1), (2)

`x = 56/11 , y = 20/11`

we get the coordinates of Orthocenter `color(blue)(O (56/11, 20/11))`

Verification

Slope `m_b = (6-1) / (3-4) = -5`

Slope of BE = -(1/m_c) = 1/5#

Equation of altitude BE is

`y - 2 = (1/5) (x - 6)`

`5y - 10 = x - 6`

`5y - x = 4` Eqn (3)

Solving equations (2) , (3),

Coordinates of `color(blue)(O (56/11, 20/11)`