Question

How do you find the vertex and intercepts for `g(x) = x^2 - 9x + 2`?

Answer 1

Vertex: `(4.5, -18.25)`
x-intercepts: `((9 + sqrt(73))/2, 0)` and `((9 - sqrt(73))/2, 0)`
y-intercept: `(0, 2)`

Explanation:

`g(x) = x^2 - 9x + 2`

This equation is in standard form, or `y = ax^2 + bx + c`.

The vertex is the highest or lowest point on the graph, depending on the coefficient (value before the `x^2` if any).

To find the vertex, we first find the `x`-value of the vertex using this equation: `x = (-b)/(2a)`.

In our equation, we know that `a = 1` and `b = -9`, so let's plug them into the equation:
`x = (-(-9))/(2(1))`
`x = 9/2` or `4.5`

Now let's find the `y`-value of the vertex. To do so, we plug in what we got for `x` into the original equation:
`g(x) = (4.5)^2 - 9(4.5) + 2`
`g(x) = 20.25 - 40.5 + 2`
`g(x) = -18.25`

So our vertex of the equation is `(4.5, -18.25)`.

---

To find the x-intercepts...
We plug in `0` for the `y`-values in the equation and solve for `x`:
`0 = x^2 - 9x + 2`

Now, to solve this, we need to use the quadratic formula, which is this long equation :(
`x = (-b+-sqrt(b^2-4ac))/(2a)`
`x = (-(-9) +- sqrt((-9)^2 -4(1)(2)))/(2(1))`
`x = (9 +- sqrt(81 - 8))/2`
`x = (9 +- sqrt(73))/2`

---

To find the y-intercepts...
We plug in `0` for the `x`-values in the equation and solve for `y`:
`g(x) = 0^2 - 9(0) + 2`
`g(x) = 0 - 0 + 2`
`g(x) = 2`

So our y-intercept is at `(0, 2)`.

---

To show that the vertex and intercepts are correct, here is a graph of this equation: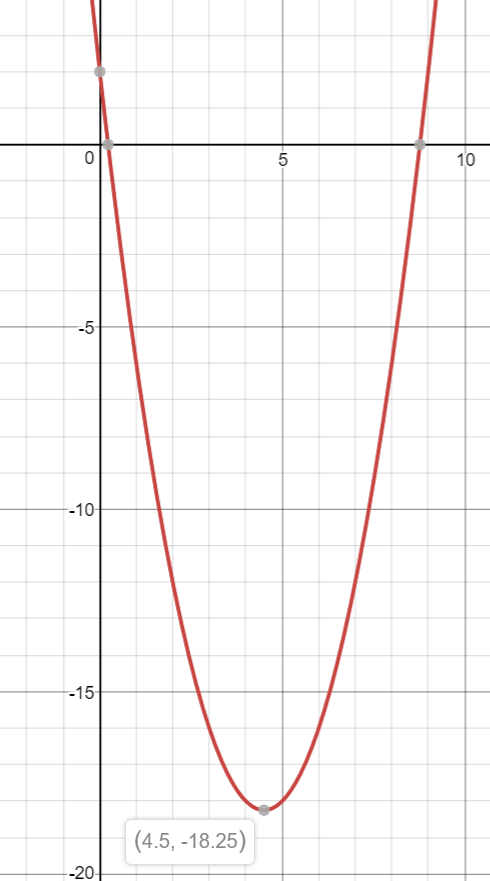

If you need more help on this type of question, feel free to watch this video:

If you need more help on quadratic formula, feel free to watch this video:

Hope this helps!