Two circles have the following equations #(x +2 )^2+(y -5 )^2= 16 # and #(x +4 )^2+(y +1 )^2= 25 #. Does one circle contain the other? If not, what is the greatest possible distance between a point on one circle and another point on the other?

Question

1330 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-01-19T13:01:18

Distance between the farthest points of the two circles is

#D_F = R_A + D + R_B = 4 + 6.3246 + 5 = color (brown)(15.3246)#

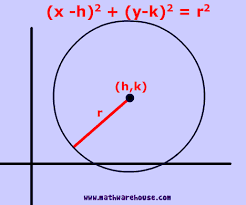
enter image source here

Standard form of equation of a circle is
#(x - h)^2 + (y-k)^2 = r^2#
Where center coordinates (h,k), r the radius.

Circle 1

#center c_1 (-2,5), radius r_1 = 4#

Circle 2

#center c_2 (-4,-1), radius r_2 = 5#

Distance between the centers

#D = sqrt((-4 - (-2))^2 + (-1-5)^) = sqrt(2^2 + 6^2) = 6.3246#

Since distance between centers greater than their radii, one circle does not contain the other.

Distance between the farthest points of the two circles is

#D_f = r_1 + D + r_2 = 4 + 6.3246 + 5 = color (brown)(15.3246)#
enter image source here