Question

How do you solve `4x-y =10`, `3x+5y=19` by graphing and classify the system?

Answer 1

`color(blue)(x= 3," " y =2)`

Explanation:

Given:

`4x-y=10" "` `color(red)(Equation.1`

`3x+5y=19" "` `color(red)(Equation.2`

Analyze the graph below for the solution:

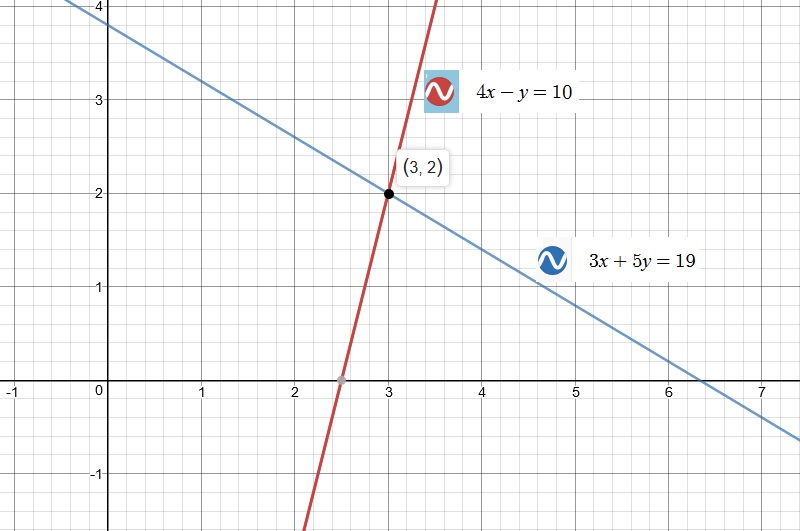
If the graphs of the equations intersect, then there is one solution that is true for both equations.

When a system has one solution (the graphs of the equations intersect once), the system is a consistent system of linear equations and the equations are independent.

We can observe that our solution

`color(blue)(x= 3," " y =2)`

satisfies the system of linear equations:

`4x-y=10" "` `color(brown)(Equation.1`

`3x+5y=19" "` `color(brown)(Equation.2`

Plug the values of `color(blue)(x=3, " "y=2" "` above to verify.

`4(3)-2=10" "` `color(green)(Equation.1`

`3(3)+5(2)=19" "` `color(green)(Equation.2`

Hence verified.