Two corners of a triangle have angles of # (3 pi )/ 8 # and # ( pi ) / 2 #. If one side of the triangle has a length of # 2 #, what is the longest possible perimeter of the triangle?

Question

1072 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-01-29T06:58:35

#P = 4.8284 + 5.2263 + 2 = color(purple)(13.0547)#

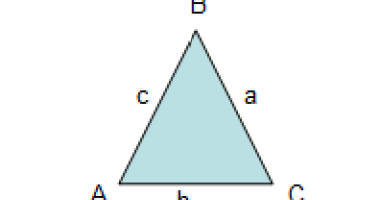
enter image source here

Given #A = (3pi)/8, B = (pi)/2#

#C = pi - (3pi)/8 - pi/2 = pi/8#

To get the longest perimeter, side 2 should correspond to the least angle #pi/8#

#a / sin ((3pi)/8) = b / sin (pi/2) = 2 / sin (pi/8)#

#a = (2 sin ((3pi)/8)) / sin (pi/8) = 4.8284#

#b = (2 sin (pi/2)) / sin (pi/8) = 5.2263#

Longest Perimeter #P = a + b + c#

#P = 4.8284 + 5.2263 + 2 = color(purple)(13.0547)#