Two corners of an isosceles triangle are at #(2 ,1 )# and #(8 ,5 )#. If the triangle's area is #4 #, what are the lengths of the triangle's sides?

Question

1472 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-02-02T02:28:28

Measure of the triangle's sides #color(violet)(7.2111, 3.7724, 3.7724)#

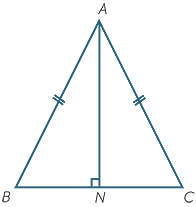
enter image source here

Length of the base (b) is the distance between the given two points (2,1) , (8,5).

Using distance formula,

#BC = a = sqrt((x2-x1)^2 + (y2-y1)^2)#

#a = sqrt((8-2)^2 + (5-1)^2) = color(green)(7.2111)#

Area of triangle #A = (1/2) a h#

#4 = (1/2) 7.2111 * h#

#AN = h = (2 * 4) / 7.2111 = color(purple)(1.1094)#

#AB = AC = b = c = sqrt((AN)^2 + (BN)^2)#

#b = c = sqrt(h^2 + (a/2)^2) = sqrt(1.1094^2 + (7.2111/2)^2) = color(red)(3.7724)#

Measure of the triangle's sides #color(violet)(7.2111, 3.7724, 3.7724)#