A point #P# moves between lines #y=0# and #y=mx# so that the area of quadrilateral formed by the two lines and perpendicular from #P# on these lines remains constant. Find the equation of locus of #P#?
1 Answer
The equation is of the locus is of type
Explanation:
Let us consider that equation of line
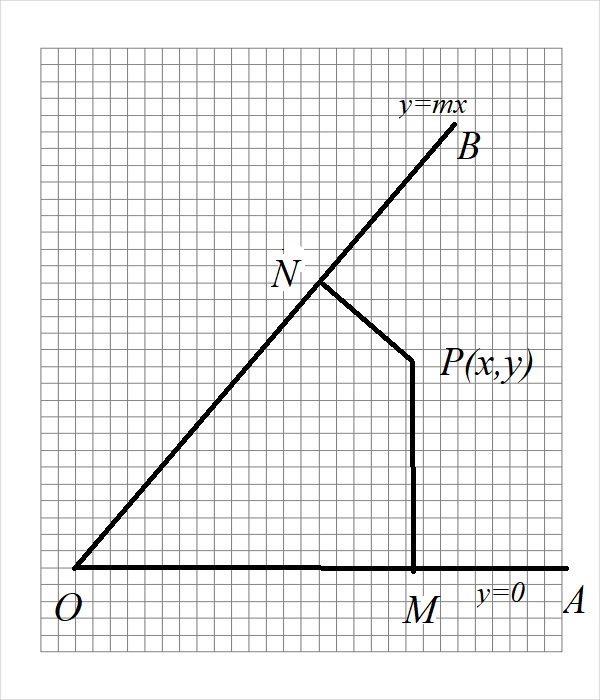
Point
Now it is evident that area of
and hence
=
=
and
Hence area of
and area of quadrilateral is
=
=
Hence equation of
This is the equation of a hyperbola.
Below is shown the graph for
graph{y^2-x^2+xy=10 [-20, 20, -10, 10]}
