Question

How do you solve `y = x^2 -8x + 16` graphically and algebraically?

Answer 1

see below

Explanation:

Graphically

the roots are where the graph crosses the `x-`axis.

that is when `y=0`

graph{x^2-8x+16 [-3.74, 14.04, -2.56, 6.33]}

As can be seen from the graph it touches the `x-`axis at one point only

`x=4`

Algebraically

we could use factorising., completing the square or the formula.

look for factorising first

`x^2-8x=16=0`

`(x-4)^2=(x-4)(x-4)=0`

`:. x-4=0=>x=4`

the repeated brackets show that we have repeated roots, and that the `x-`axis is a tangent to the graph.

Answer 2

`y = x^2 - 8x + 16`

Let's solve it algebraically first:

We solve this by finding the "zeros" or x-intercepts of the equation. To do this, we factor the equation, if possible.

We need to find 2 numbers (can be the same) that add up to `-8` and multiply to `16`.
`-4` works:
`-4 + -4 = -8`
`-4 * -4 = 16`

So our equation is:
`y = (x-4)(x-4)` or `y = (x-4)^2`

Since we are finding the x-intercept(s), let's set `y = 0`. So:
`0 = (x-4)^2`

To simplify this, let's root both sides by `2`:
`sqrt(0) = sqrt((x-4)^2)`

`0 = x-4`

`x = 4`

So the x-intercept is at `(4, 0)`.

---

To graph this, we find the vertex and the slope.

In this case, since there is only one x-intercept, that means that it is the vertex.

The slope depends on the coefficient, or the number in front of the highest degree term.
`x^2` means `1x^2`, so our slope is one.

Let's graph this now!

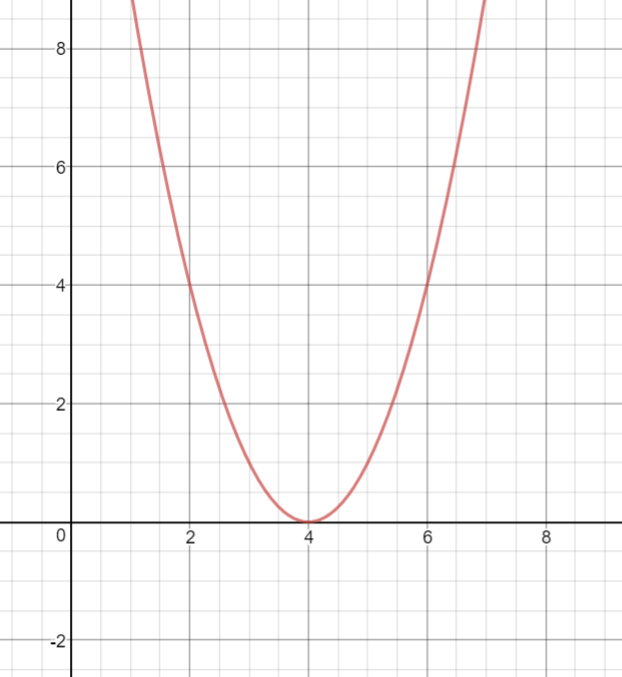
As you can see, the x-intercept is the same as the vertex.

Hope this helps!