How do you solve #y = x^2 -8x + 16# graphically and algebraically?
2 Answers
see below
Explanation:
Graphically
the roots are where the graph crosses the
that is when
graph{x^2-8x+16 [-3.74, 14.04, -2.56, 6.33]}
As can be seen from the graph it touches the
Algebraically
we could use factorising., completing the square or the formula.
look for factorising first
the repeated brackets show that we have repeated roots, and that the
Let's solve it algebraically first:
We solve this by finding the "zeros" or x-intercepts of the equation. To do this, we factor the equation, if possible.
We need to find 2 numbers (can be the same) that add up to
So our equation is:
Since we are finding the x-intercept(s), let's set
To simplify this, let's root both sides by
So the x-intercept is at
To graph this, we find the vertex and the slope.
In this case, since there is only one x-intercept, that means that it is the vertex.
The slope depends on the coefficient, or the number in front of the highest degree term.
Let's graph this now!
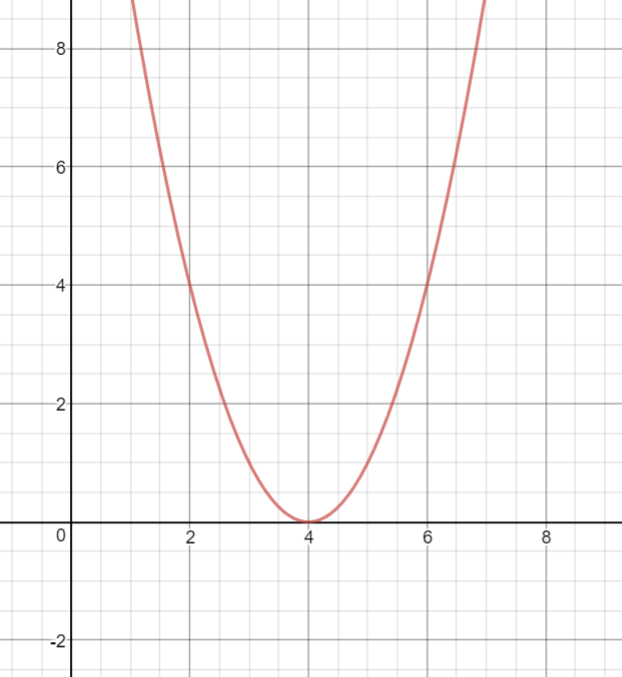
As you can see, the x-intercept is the same as the vertex.
Hope this helps!


