Question

How do you evaluate `arctan(1)` without a calculator?

Answer 1

`arctan(1)\ \ =\ \ pi/4` `" "` or `" "` `arctan(1)\ \ =\ \ 45^{\circ}`

``

Explanation:

``
``

`arctan(1)\ \ =\ \ pi/4` `" "` or `" "` `arctan(1)\ \ =\ \ 45^{\circ}`

Answer 2

`arctan(1)=pi/4=45^@`

Explanation:

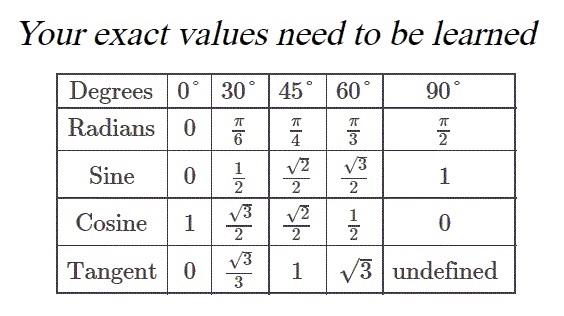
Alternative you can draw it

I have drawn it in free hand,
so i hope you can see what it represents

It is the 1. quadrant of the unit circle,
both the leg of the triangle must be 1,
and thus the two remaining angles must be the same
that is `theta=arctan(1)=pi/4=45^@`