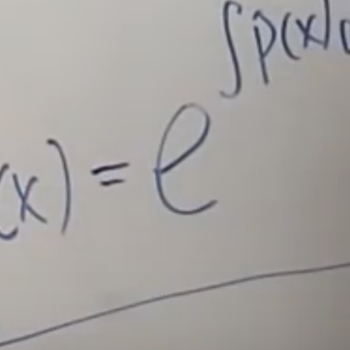How do you integrate 3/((x-2)(x+1)) using partial fractions?
2 Answers
Explanation:
In order to integrate the function, we first use partial fractions to split the integrand
Now integrating, we get
Explanation:
Partial Fractions
Multiply the whole equation by
expand the brackets
factorise
and
So
and
subtract equation
Substitute
or
Integration
because of the constant multiple of -1
Evaluate the two integrals separately
use u-substitution
Bring the integral into the u world
Bring back into the x world
second integral
use another letter substitution so you or the marker doesn't get confused
bring the integral into the v world
bring back into the x world
A negative constant, adding or subtracting a constant from another constant is still a constant so we will just make another constant
Use the log law
put the parts of the integral that we answered back together