How would I answer this question about charges?
Given #q_1=2q_2=3q_3=4nC# , and each charge is #1 cm# away from the origin, what is the electric field magnitude at the origin?
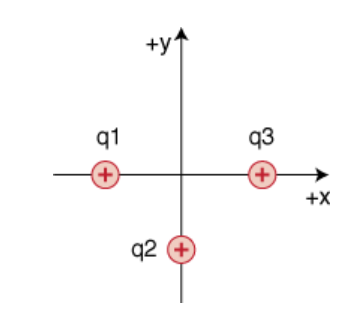
Given

1 Answer
Explanation:
Electric Field:
We simply sum the fields of the three charges at the origin.
Charge q1:
Charge q2:
Charge q3:
The field at the origin:
when


