Question

How do you solve `x^2+5x+6>0`?

Answer 1

`x_1> -2 or x_2< -3`

Explanation:

`x^2+5x+6>0`
`color(blue)(x^2+2*5/2x+(5/2)^2)-(5/2)^2+6>0`
`color(blue)((x+5/2)^2)-25/4+6>0`
`(x+5/2)^2-1/4>0 |+1/4`
`(x+5/2)^2>1/4|sqrt()`
`x+5/2>+-1/2|-5/2`

`x_1> -2 or x_2< -3`

If you struggle to understand any of the steps I made,
feel free to write a comment :)

Answer 2

Range satisfying the given condition: `color(blue)(x<(-3) or x >(-2)`

We can also write the solution using the interval notation as:

`color(blue)((-oo,-3) uu (-2, oo)`

Explanation:

Given:

We are given the inequality:

`color(red)(x^2+5x+6>0`

`color(purple)("Step 1")`

Write this inequality as `color(green)(x^2+5x+6=0` to factorize.

Consider the quadratic expression `x^2+5x+6`

Split the middle term to factorize as shown below:

We want two numbers that multiply together to make 6, and add up to 5.

`x^2+3x+2x+6`

Factor the first two terms and the last two terms separately:

`x(x+3)+2(x+3)`

Observe that `(x+3)` is a common factor to both the terms.

Hence, we can write our factors as `color(blue)((x+3)(x+2)`

`color(purple)("Step 2")`

We will construct the sign chart:

`(i)` Compute the signs of `(x+2):`

`x+2=0`

Add `color(red)(-2` to both sides of the equation.

`x+2+color(red)((-2))=0+color(red)((-2)`

`x+cancel 2+color(red)((-cancel 2))=0+color(red)((-2)`

`x=-2`

Hence, `x+2` is ZERO for `x=-2`

Similarly, `(x+2)` is negative for `x < -2`

`(x+2)` is positive for `x > -2`

`color(purple)("Step 3")`

`(ii)` Compute the signs of `(x+3):`

`x+3` is ZERO for `x=-3`

`x+3` is negative for `x<(-3)`

`x+3` is positive for `x>(-3)`

We will summarize and create a table of values.

Hence,

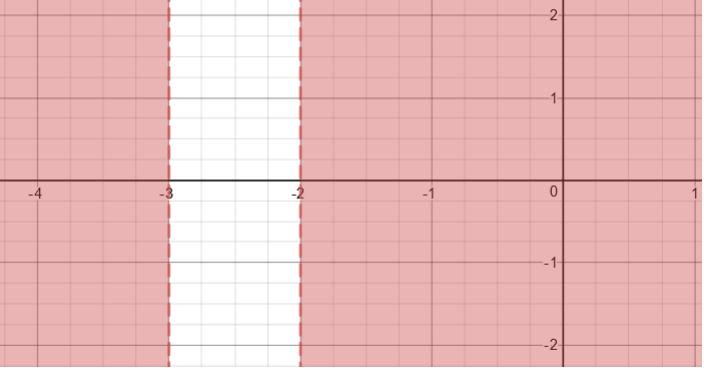
Range satisfying the given condition: `color(blue)(x<(-3) or x >(-2)`

We can also write the solution using the interval notation as:

`color(blue)((-oo,-3) uu (-2, oo)`

An image of the graph for the inequality is available below:

Hope it helps.