How do you find the vertex and intercepts for #y = 5(x+2)^2 + 7#?
1 Answer
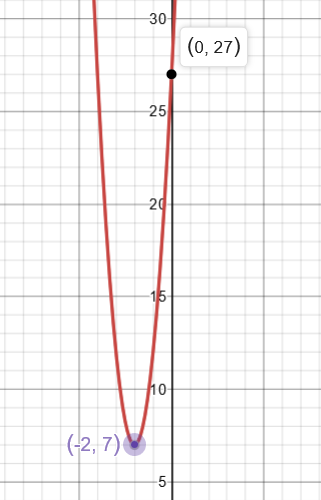
Vertex of the parabola formed by
x-intercept: Does not exist.
y-intercept:
Explanation:
Standard form of a quadratic function is
The parabola will open up , if the the coefficient of
The parabola will open down , if the the coefficient of
Let us consider the quadratic function given to us:
Using the algebraic identity
We have seen that
Standard form of a quadratic function is
Note that,
To find the x-coordinate of the Vertex, use the formula
To find the y-coordinate of the vertex, substitute
Hence, Vertex is at
Since, the coefficient of the
x-intercept is a point on the graph where
Solve
Subtract
Divide both sides by
Observe that
y-intercept is the point on the graph where
Hence,
Vertex of the parabola formed by:
is
x-intercept: Does not exist.
y-intercept:
An image of the graph is available below: