Question

The area under the curve y=e^-x between x=0 and x=1 is rotated about the x axis find the volume?

Answer 1

Volume is `pi/2(1-e^-2)=1.358` cubic units.

Explanation:

Let us see the graph of `y=e^(-x)` between `x=0` and `x=1`.

graph{e^(-x) [-2.083, 2.917, -0.85, 1.65]}

To find the desired volume the shaded portion (shown below, will have to be rotated around `x`-axis.

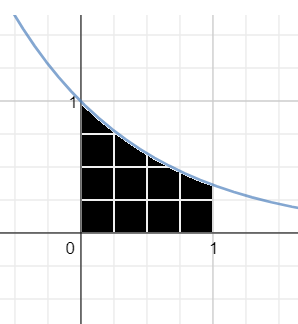
As volume of a cylinder is `pir^2h`, here we will have `r=e^(-x)` and `h=dx`

and hence volume would be

`int_0^1pie^(-2x)dx`

= `piint_0^1e^(-2x)dx`

= `pixx[-e^(-2x)/2]_0^1`

= `pi[-e^(-2)/2+1/2]`

= `pi/2(1-e^-2)`

= `pi/2(1-0.1353)`

= `1.358`