Question

How do you find the value of `tan(csc^-1(2))`?

Answer 1

`sqrt3`

Explanation:

First you need to find the angle that corresponds to a csc value of 2, which is what inverse csc is doing.
`csc^-1=1/(cos^-1)= 2`
`cos^-1 = 1/2`
So find when cos is 1/2, which is at `pi/3`
Then plug in `pi/3` for `csc^-1(2)`
Evaluate `tan(pi/3)`
`tan(pi/3) = sqrt3`

Answer 2

Use the identity:

`tan(csc^-1(x)) = 1/sqrt(x^2-1)`

Explanation:

Please see this reference section Relationships between trigonometric functions and inverse trigonometric functions. I am referring you to this section because it contains a table that will help you if your current studies require you to do many problems of this type.

The table gives the following identity:

`tan(csc^-1(x)) = 1/sqrt(x^2-1)`

Please notice that there is a nice triangle drawing to the right within the table:

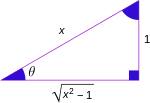
Substitute `x = 2` into the identity:

`tan(csc^-1(2)) = 1/sqrt(2^2-1)`

`tan(csc^-1(2)) = 1/sqrt(4-1)`

`tan(csc^-1(2)) = 1/sqrt(3)`

Rationalize the denominator:

`tan(csc^-1(2)) = sqrt(3)/3`