What is the orthocenter of a triangle with corners at #(2 ,7 )#, #(1 ,1 )#, and (3 ,2 )#?
1 Answer
Please read the explanation.
Explanation:
The altitude of a triangle is a perpendicular line segment from the vertex of the triangle to the opposite side.
The Orthocenter of a triangle is the intersection of the three altitudes of a triangle.
Construct the triangle
Vertices
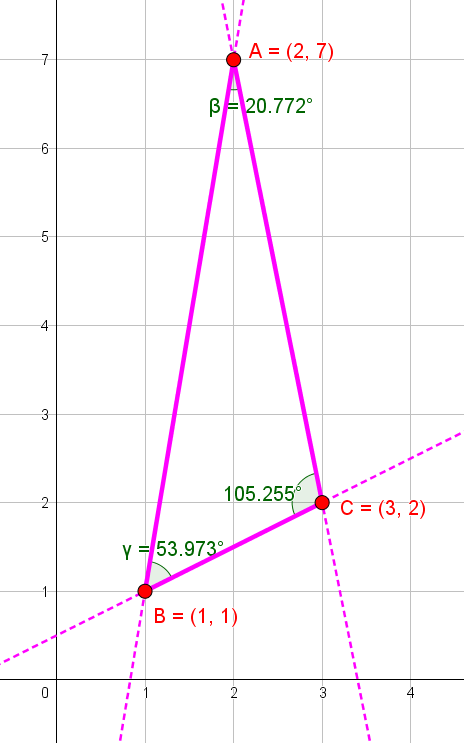
Observe that
This angle is greater than
If the triangle is an obtuse triangle, the Orthocenter lies outside the triangle.
Construct altitudes through the vertices of the triangle as shown below:
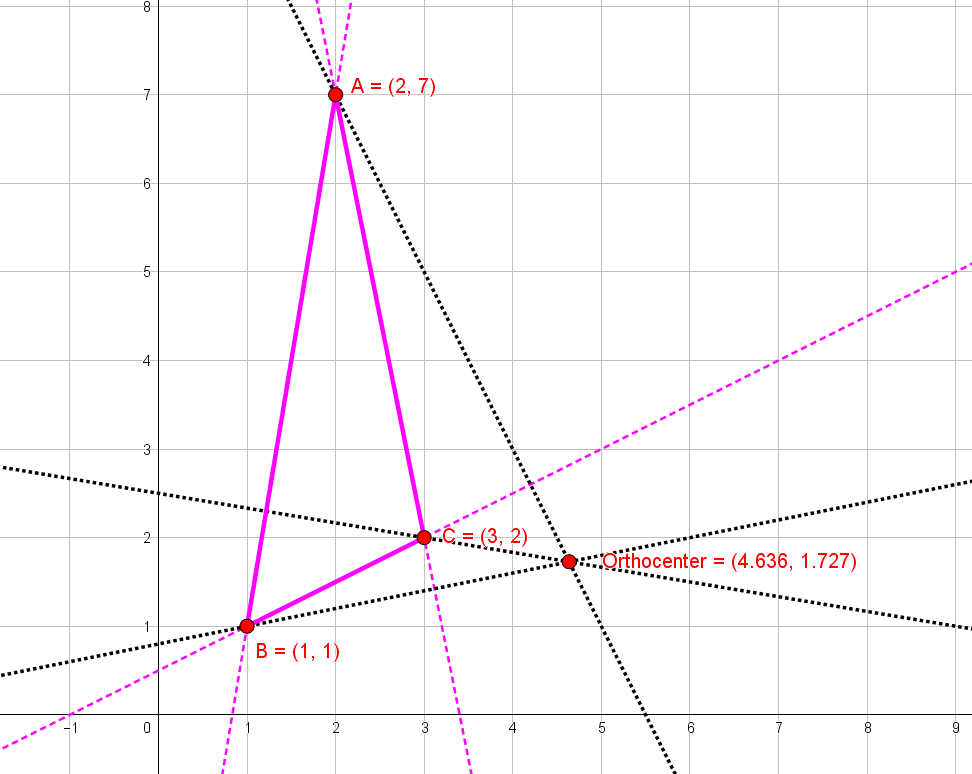
All the three altitudes meet at a point referred to as the Orthocenter.
Since the triangle is obtuse, the orthocenter lies outside the triangle.
Observe that the Orthocenter has
Hope it helps.

