A cow is tied to a silo with radius r by a rope just long enough to reach the opposite side of the silo. Find the grazing area available for the cow?
 computer
computer
Edit: I found this, would that work in solving the problem?
computer
Edit: I found this, would that work in solving the problem?
1 Answer
Explanation:
First, we need to know the length of rope, and we know the rope can reach the opposite side of the silo.
By letting the length of the rope be
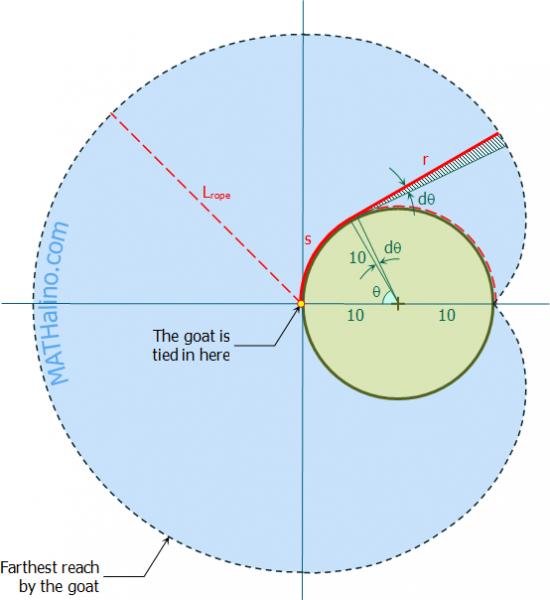 https://www.mathalino.com/reviewer/integral-calculus/area-grazing-goat-tied-silo
https://www.mathalino.com/reviewer/integral-calculus/area-grazing-goat-tied-silo
This picture depicts the area the cow can graze and ignore the
Now to find the area we shall split it into 2 portions,
-
The semicircle on the left of the diagram
-
The circle involute on the right of the diagram
1. To find the semicircle,
Find area of the semicircle
A_1=1/2*pi(pir)^2
color(white)(a)=1/2pi^3r^2
https://www.mathalino.com/reviewer/integral-calculus/area-grazing-goat-tied-silo
2. To find the circle involute,
Find the length of wrapped rope
s ,
s=rtheta Find the length of unwrapped rope
r ,
r=l-s
color(white)(r)=pir-rtheta
color(white)(r)=r(pi-theta) Find the area of the circle involute,
A_2=|1/2int_0^pir^2d theta|
color(white)(A_2)=|1/2int_0^pi r^2(pi-theta)^2 d theta|
color(white)(A_2)=|r^2/2[(pi-theta)^3/3]_0^pi|
color(white)(A_2)=|r^2/6[(pi-pi)^3-(pi-0)^3]|
color(white)(A_2)=|-(pi^3r^2)/6|
color(white)(A_2)=(pi^3r^2)/6
https://www.mathalino.com/reviewer/integral-calculus/area-grazing-goat-tied-silo
Now, we can find the total area,
Therefore, the grazing area for the cow is

