Question

A cow is tied to a silo with radius `r` by a rope just long enough to reach the opposite side of the silo. Find the grazing area available for the cow?

Edit: I found this, would that work in solving the problem?

Answer 1

`5/6pi^3r^2`

Explanation:

First, we need to know the length of rope, and we know the rope can reach the opposite side of the silo.

By letting the length of the rope be `l`,

`l=1/2*2pir`
`color(white)(l)=pir`

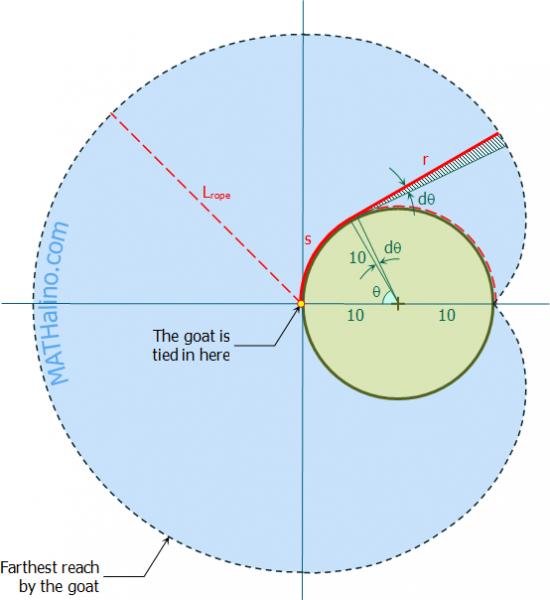
This picture depicts the area the cow can graze and ignore the `10` and replace it with `r`.

Now to find the area we shall split it into 2 portions,

1. The semicircle on the left of the diagram

2. The circle involute on the right of the diagram

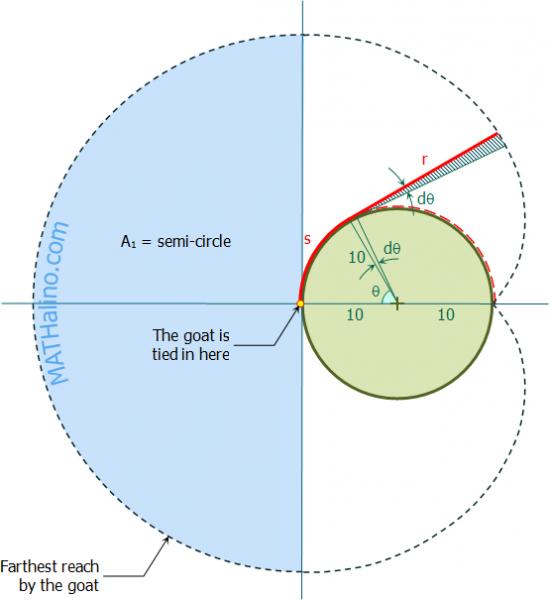
1. To find the semicircle,

Find area of the semicircle

`A_1=1/2*pi(pir)^2`
`color(white)(a)=1/2pi^3r^2`

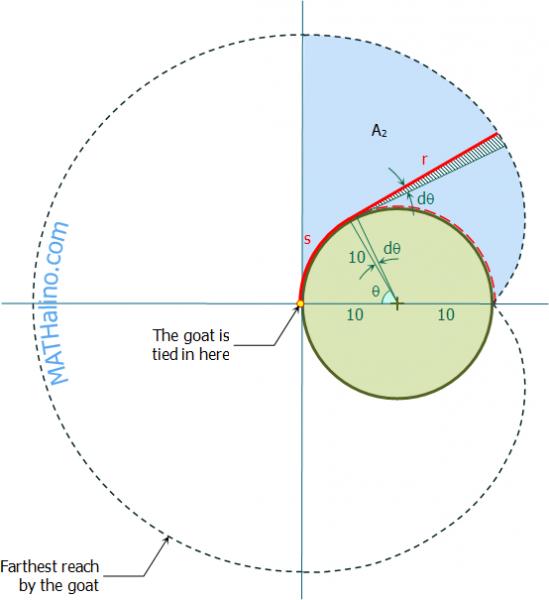
2. To find the circle involute,

Find the length of wrapped rope `s`,

`s=rtheta`

Find the length of unwrapped rope `r`,

`r=l-s`
`color(white)(r)=pir-rtheta`
`color(white)(r)=r(pi-theta)`

Find the area of the circle involute,

`A_2=|1/2int_0^pir^2d theta|`
`color(white)(A_2)=|1/2int_0^pi r^2(pi-theta)^2 d theta|`
`color(white)(A_2)=|r^2/2[(pi-theta)^3/3]_0^pi|`
`color(white)(A_2)=|r^2/6[(pi-pi)^3-(pi-0)^3]|`
`color(white)(A_2)=|-(pi^3r^2)/6|`
`color(white)(A_2)=(pi^3r^2)/6`

Now, we can find the total area,

`A=A_1+2A_2`
`color(white)(A)=1/2pi^3r^2+2((pi^3r^2)/6)`
`color(white)(A)=1/2pi^3r^2+1/3pi^3r^2`
`color(white)(A)=5/6pi^3r^2`

Therefore, the grazing area for the cow is `5/6pi^3r^2`.