Question

Prove the following statement. Let ABC be any right triangle, the right angle at point C. The altitude drawn from C to the hypotenuse splits the triangle into two right triangles that are similar to each other and to the original triangle?

Answer 1

See Below.

Explanation:

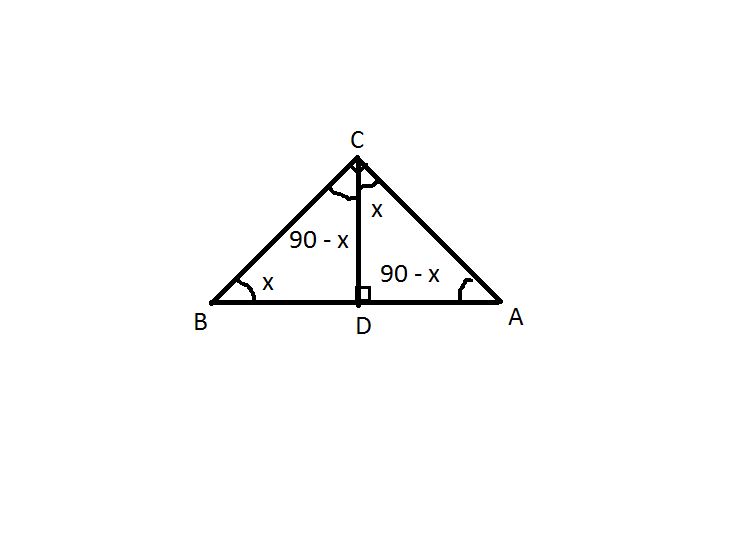
According to the Question,

`DeltaABC` is a right triangle with `/_C = 90^@`, and `CD` is the altitude to the hypotenuse `AB`.

Proof:

Let's Assume that `/_ABC = x^@`.

So, `angleBAC = 90^@- x^@ = (90 - x)^@`

Now, `CD` perpendicular `AB`.

So, `angleBDC = angleADC = 90^@`.

In `DeltaCBD`,

`angleBCD = 180^@ - angleBDC - angleCBD = 180^@ - 90^@ - x^@ = (90 -x)^@`

Similarly, `angleACD = x^@`.

Now, In `DeltaBCD` and `DeltaACD`,

`angle CBD = angle ACD`

and `angle BDC = angleADC`.

So, by AA Criteria of Similarity, `DeltaBCD ~= DeltaACD`.

Similarly, We can find, `DeltaBCD ~= DeltaABC`.

From that, `DeltaACD ~= DeltaABC` .

Hope this helps.