The situation we have here can be visualised below:
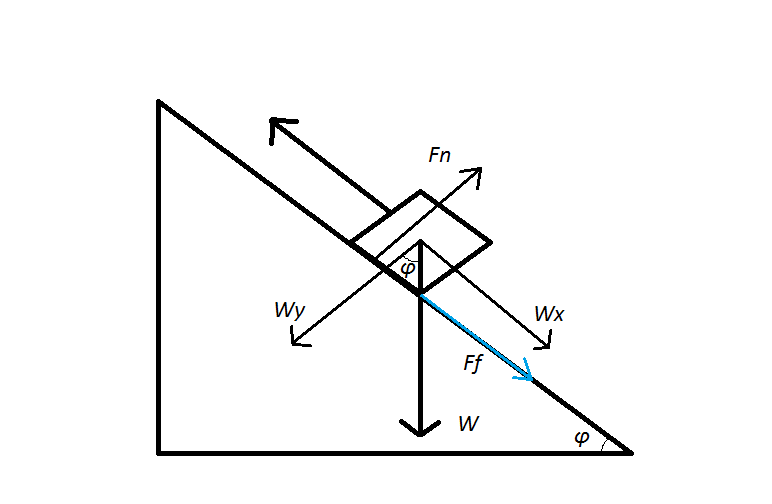
First of all, let's define what everything is; #F_f# is the friction force, #F_n# is the normal force, #W# is the weight and #varphi# is the angle at which the ramp is inclined at.
Note: The big arrow symbolises movement, not a force.
Now, we usually want to have our forces have the same direction, but in the case of the inclined plane, the weight #W# doesn't really behave nicely, which is why we instead break it down into #W_x# and #W_y#, forces which are parallel to the hypotenuse of the ramp and perpendicular to it, respectively.
These are not random, however. They have the property that
#vec (W_x)+vec(W_y)=vecW#
Also, the angle between #W_y# and #W# is #varphi# due to the similarity of the triangles.
As it isn't stated, we assume that no force is pushing the object.
In order to solve this, we have to use the variation of Mechanical Energy. That, or the variation of Kinetic Energy, but I think that that's a bit more complicated.
Let #E# be the mechanical energy, #E_k# be the kinetic energy and #E_p# be the gravitational potential energy.
The variation of mechanical energy, #Delta E#, is:
#Delta E=w_("ext")=E_f-E_i#
where #w# is the work.
What does this mean? Well, it means that if an object moves from point #A# to point #B#, the mechanical energy of is changed by a quantity #DeltaE#, which equal to the work of all the external forces in the system. An external force is one that arises from outside of the system, for example #F_f#.
Let's get into the juicy part.
We have initial velocity #v_i=5m"/"s# and initial height #h_i =0#. When the box reaches the point of maximum height, its velocity is #v_f = 0# and its height #h_("max")#. Using the variation of mechanical energy, we have:
#Delta E = w_("ext") = Fs#, where #s# is the displacement; what we want to find.
Now, the only forces which act on the direction of movement are the forces #F_f# and #W_x#. As they act against it, the work will negative.
#Delta E = -(F_f+W_x)s#
Since the variation of energy is just #E_("final") - E_("initial")#, we have:
#E_f-E_i = -(F_f+W_x)s#
Knowing that the mechanical energy in a point #C# is
#E_c = E_(kC)+E_(pC)#
We can deduce that #E_f# is comprised totally of the potential energy at that point; this is due to the fact that the velocity #v_f#. Similarly, #E_i# is only made up of kinetic energy.
#:. E_(pf)-E_(ci) = -(F_f+W_x)s#
Let's start calculating everything:
#E_(pf) = mgh_("max")#
#E_(ci)=(mv_i^2)/2=(25m)/2#
#F_f = F_nmu#
Where #mu# is the coefficient of friction. At the same time, #F_n = W_y# due to the fact they are opposite and that the box is not moving vertically (perpendicular to the ramp, that is)
#F_f = W_y*1/2#
In our triangle, we can get the following results:
#sin varphi=W_x"/"W=> W_x=Wsinvarphi#
#cosvarphi = W_y"/"W => W_y=Wcosvarphi#
As #varphi = (2pi)/3#:
#W_x=sqrt3/2W and W_y=1/2W#
#=> F_f = 1/4W=1/4mg#
About #h_max#, we can get that #h_max=ssinvarphi#
Hence, we get:
#cancelm(sqrt3/2gs-25/2)=-cancelm(1/4g+sqrt3/2g)s#
We can see that the mass #m# doesn't matter, as it is simplified.
Now, get everything featuring #g# and #s# on the left hand side:
#sqrt3/2gs+1/4gs+sqrt3/2gs=25/2#
#gs(sqrt3+1/4)=25/2#
#gs(4sqrt3+1)=50#
#color(red)( :.s=50/(g(4sqrt3+1)) ~~ 0.6306#

