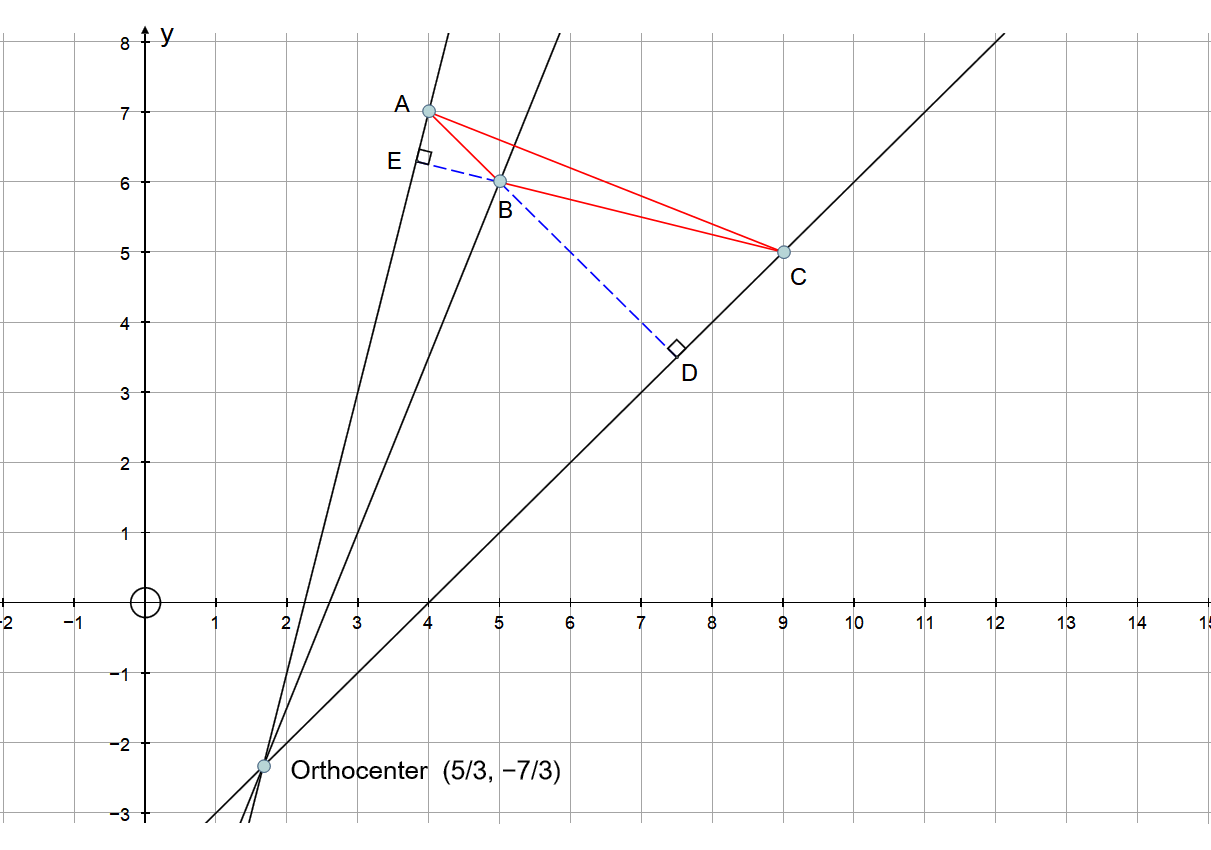
What is the orthocenter of a triangle with corners at #(4 ,7 )#, #(9 ,5 )#, and #(5 ,6 )#?
1 Answer
Explanation:
The orthocenter is the point where the extended altitudes of a triangle meet. This will be inside the triangle if the triangle is acute, outside of the triangle if the triangle is obtuse. In the case of the right angled triangle it will be at the vertex of the right angle. ( The two sides are each altitudes ).
It is generally easier is you do a rough sketch of the points so you know where you are.
Let
Since the altitudes pass through a vertex and are perpendicular to the side opposite, we need the find the equations of these lines. It will be obvious from the definition that we only need to find two of these lines. These will define a unique point. It is unimportant which ones you choose.
I will use:
Line
Line
For
First find the gradient of this line segment:
A line perpendicular to this will have a gradient that is the negative reciprocal of this:
This passes through
For
Passing through
The intersection of
Solving simultaneously:
Substituting in
Orthocenter:
Notice the the orthocenter is outside the triangle because it is obtuse. The altitude lines passing through