Two corners of an isosceles triangle are at #(8 ,2 )# and #(4 ,3 )#. If the triangle's area is #9 #, what are the lengths of the triangle's sides?
2 Answers
Explanation:
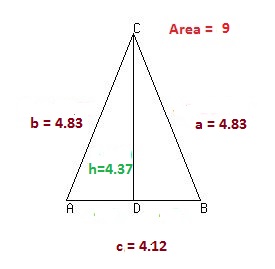
Base
Explanation:
They're vertices, not corners. Why do we have the same bad wording of the question from all around the world?
Archimedes' Theorem says if
For an isosceles triangle,
We're not sure if the given side is
If we started with
No real solutions for that one.
We conclude we have base

