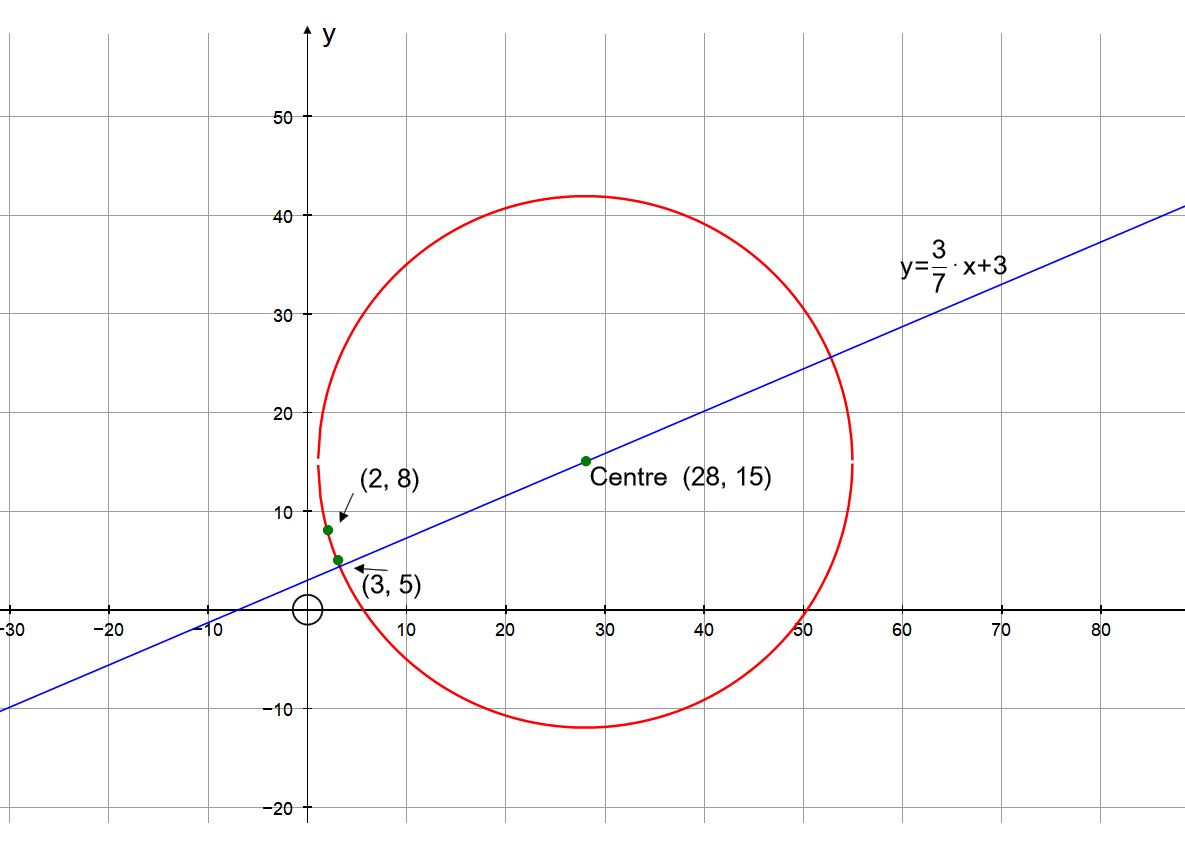
A circle has a center that falls on the line #y = 3/7x +3 # and passes through # ( 2 ,8 )# and #(3 ,5 )#. What is the equation of the circle?

Question

1451 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-06-17T15:29:31

#color(blue)((x-28)^2+(y-15)^2=725#

The standard form of the equation of a circle is given as:

#(x-h)^2+(y-k)^2=r^2#

Where:

#bbh# and #bbk# are the #bbx# and #bby# co-ordintates of the centre respectively, and #bbr# is the radius.

If the centre lie on the line #y=3/7x+3#, then #bbh# and #bbk# lie on this line:

#:.#

#k=3/7h+3 \ \ \ \[1]#

We are given two points on the circumference of the circle:

#(2,8), (3,5)#

Using: #(x-h)^2+(y-k)^2=r^2#

#(2-h)^2+(8-k)^2=r^2 \ \ \ \[2]#

#(3-h)^2+(5-k)^2=r^2 \ \ \ \[3]#

Solving simultaneously:

#[2] - [3]#

#-5+2h+39-6k=0#

#34+2h-6k=0#

#k=1/3h+17/3 \ \ \ [4]#

#"substituting " [1] " in " [4]#

#3/7h+3=1/3h+17/3#

#3/7h+3-1/3h-17/3=>h=28#

In #[1]#

#k=3/7(28)+3=15#

Centre of circle is at #(28,15)#

Using this and point #(3,5)#, we have:

#r^2=(3-28)^2+(5-15)^2=725#

Equation of circle is:

#color(blue)((x-28)^2+(y-15)^2=725#

PLOT:

enter image source here