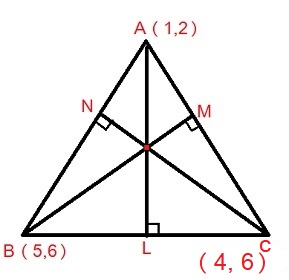
Let , #triangleABC# be the triangle with corners at
#A(1,2) , B(5,6) andC(4,6)#
Let , #bar(AL), bar(BM) and bar(CN) # be the altitudes on sides
#bar(BC), bar(AC) andbar(AB)# respectively .
Let #(x,y)# be the intersection of three altitudes .
Slope of #bar(AB)#=#(6-2)/(5-1)=1=>#slope of #bar(CN)=-1#[#:.# altitude ] and #bar(CN)# passes through #C(4,6)#
So, equn. of #bar(CN)# is :#y-6=-1(x-4)#
#i.e. color(red)(x+y=10....to (1)#
Now,
Slope of #bar(AC)#=#(6-2)/(4-1)=4/3=>#slope of #bar(BM)#=#-3/4#[#:.# altitude ]
and #bar(BM)# passes through #B(5,6)#
So,
equn. of #bar(BM)# is :#y-6=-3/4(x-5)=>4y-24=-3x+15#
#i.e. color(red)(3x+4y=39....to (2)#
From equn. #(1)# we get ,#color(red)(y=10-x to(3)#
putting #y=10-x # into #(2)#
#3x+4(10-x)=39#
#=>3x+40-4x=39#
#-x=-1=>color(blue)(x=1#
From #(3)# we have
#y=10-1=>color(blue)(y=9#
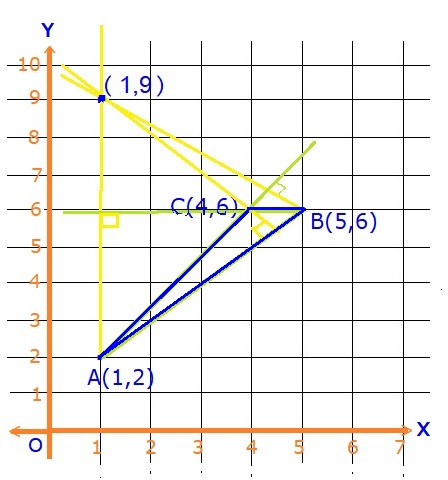
Hence, orthocenter of triangle is :(1,9)
Please see the graph below: