A triangle has corners A, B, and C located at #(4 ,2 )#, #(2 ,6 )#, and #(8 ,4 )#, respectively. What are the endpoints and length of the altitude going through corner C?

2 Answers
Harish Chandra Rajpoot
Jul 27, 2018

Length of altitude #=2\sqrt5# & end-points of altitude #(8, 4)# & #(4, 2)#

Explanation:

The vertices of #\Delta ABC# are #A(4, 2)#, #B(2, 6)# & #C(8, 4)#

The area #\Delta# of #\Delta ABC# is given by following formula

#\Delta=1/2|4(6-4)+2(4-2)+8(2-6)|#

#=10#

Now, the length of side #AB# is given as

#AB=\sqrt{(4-2)^2+(2-6)^2}=2\sqrt5#

If #CN# is the altitude drawn from vertex #C# to the side #AB# then the area of #\Delta ABC# is given as

#\Delta =1/2(CN)(AB)#

#10=1/2(CN)(2\sqrt5)#

#CN=2\sqrt5#

Let #N(a, b)# be the foot of altitude CN drawn from vertex #C(8, 4)# to the side #AB# then side #AB# & altitude #CN# will be normal to each other i.e. the product of slopes of AB & CN must be #-1# as follows

#\frac{b-4}{a-8}\times \frac{6-2}{2-4}=-1#

#a=2b\ ............(1)#

Now, the length of altitude CN is given by distance formula

#\sqrt{(a-8)^2+(b-4)^2}=2\sqrt5#

#(2b-8)^2+(b-4)^2=(2\sqrt5)^2#

#(b-4)^2=4#

#b=6, 2#

Setting these values of #b# in (1), we get the corresponding values of #a# as follows

#a=2\times 6=12\ \ & \ \ \ a=2(2)=4#

#a=12, 4#

The endpoints of altitude from vertex #C(8, 4)# are #(12, 6)#
& #(4, 2)# But #(12, 6)# is not the end point of altitude.

hence, the end points of altitude from vertex #C# are

#(8, 4), (4, 2)#

maganbhai P.
Jul 27, 2018

#A(4,2) and C(8,4) # are the endpoints of altitude.

Length of the altitude #=AC=2sqrt5#

Explanation:

Let , #triangle ABC" be the triangle with corners at"#

#A(4,2) , B(2,6) and C(8,4)#

#"Using "color(blue)"Distance formula :"#

Distance between two points #P(x_1,y_1) and Q(x_2,y_2)# is :

#color(blue)(PQ=sqrt((x_1-x_2)^2+(y_1-y_2)^2)#

#AB=sqrt((4-2)^2+(2-6)^2)=sqrt(4+16)=sqrt20#

#BC=sqrt((8-2)^2+(4-6)^2)=sqrt(36+4)=sqrt40#

#AC=sqrt((4-8)^2+(2-4)^2)=sqrt(16+4)=sqrt20#

#i.e. (AB)^2=20 , (BC)^2=40 and (AC)^2=20#

#:.(AB)^2+(AC)^2=(BC)^2=40#

#:.triangle ABC " is Right Triangle" =>mangle A=90^circ#

So , #A(4,2) "is the Orthocenter of" triangle ABC"#

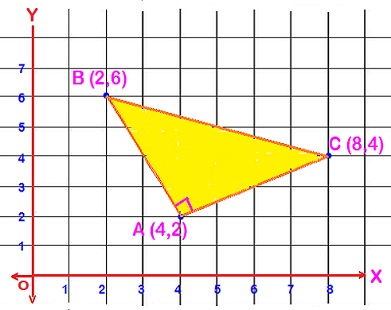
enter image source here

It is clear that , #bar(AC)# is the altitudes of #triangle ABC ,# going through

corner #C(8,4).#

So, #A(4,2) and C(8,4) # are the endpoints of altitude.

Length of the altitude #=AC=sqrt20=2sqrt5#

Related questions
See all questions in Altitudes
Impact of this question
1651 views around the world
You can reuse this answer
Creative Commons License