Question

How do you find the slope and intercept of `y = -5x + 2`?

Answer 1

Slope: `-5`

`x`-intercept: `(2/5, 0)`

`y`-intercept: `(0, 2)`

Explanation:

`y = -5x + 2`

This equation is in slope-intercept form:

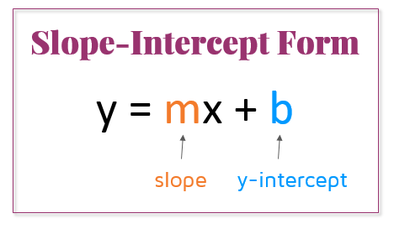
Based on the image, we know that the slope is the value multiplied by `x`, so the slope is `-5`.

To find the `x`-intercept, plug in `0` for `y` and solve for `x`:
`0 = -5x + 2`

Subtract `color(blue)2` from both sides:
`0 quadcolor(blue)(-quad2) = -5x + 2 quadcolor(blue)(-quad2)`

`-2 = -5x`

Divide both sides by `color(blue)(-5)`:
`(-2)/color(blue)(-5) = (-5x)/color(blue)(-5)`

`2/5 = x`

`x = 2/5`

The `x`-intercept is at `(2/5, 0)`.

To find the `y`-intercept, plug in `0` for `x` and solve for `y`:
`y = -5(0) + 2`

`y = 0 + 2`

`y = 2`

The `y`-intercept is at `(0, 2)`.

Hope this helps!

Answer 2

Slope `-5`, `x`-int `2/5`, `y`-int `2`

Explanation:

The good thing is that this equation is in slope-intercept form

`y=mx+b`, with slope `m` and a `y`-intercept of `b`. With this in mind, we see that our slope is `-5` and our `y`-intercept is `2`.

What about the `x`-intercept?

The `x`-intercept is the value when `y=0`. We can plug this into our equation to get

`0=-5x+2`

`-5x=-2=>x=2/5`

Therefore, our slope is `-5`, our `x`-intercept is `2/5` and our `y`-intercept is `2`.

Hope this helps!