How do you solve the system by graphing #y = 2x + 1# and #y = 2x - 2#?

Question

9506 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-08-11T12:49:06

The system of linear equation are inconsistent.
The inconsistent system has no solution.

We have , both the eqn. are in Slop-intercept form:

#y=2x+1 ....to(1) and y=2x-2....to(2)#

#(1)#Draw value table for #: y=2x+1#

#ul(|x=|color(white)(,.,)0 | color(white)(.....)1|color(white)(...)-2|#
#ul(|y=|color(white)(,..)1|color(white)(.....)3|color(white)(...)-3|#

#(2)#Draw value table for #: y=2x-2#

#ul(|x=|color(white)(,.,)0 | color(white)(.....)2|color(white)(...)-1|#
#ul(|y=|color(white)(.)-2|color(white)(.....)2|color(white)(...)-4|#

Plot the graph of both equations.

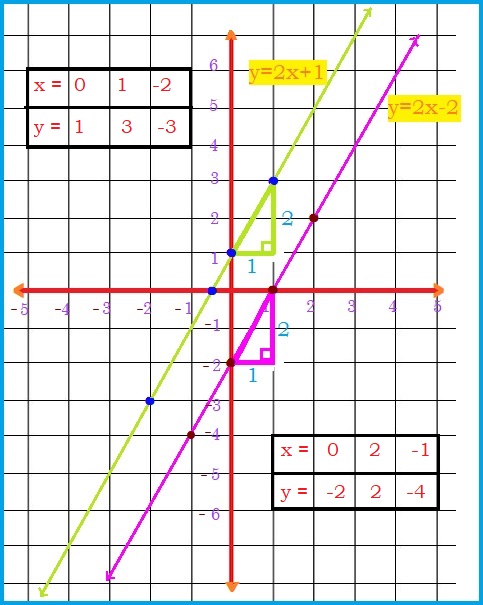
enter image source here

We can see that both the lines are parallel and never intersect each other.

The system of linear equation are inconsistent.

The inconsistent system has no solution.