A triangle has corners A, B, and C located at #(4 ,5 )#, #(3 ,6 )#, and #(8 ,4 )#, respectively. What are the endpoints and length of the altitude going through corner C?

Question

1679 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-08-14T10:16:25

#N(13/2,5/2) and C(8,4)# are the endpoints of altitudes
going through corner #C#
The length of the altitude #=:.CN=3/sqrt2~~2.12#

Let #triangleABC " be the triangle with corners at"#

#A(4,5), B(3,6) and C(8,4)#

Let #bar(AL) , bar(BM) and bar(CN)# be the altitudes of sides #bar(BC) ,bar(AC) and bar(AB)# respectively.

Let #(x,y)# be the intersection of three altitudes

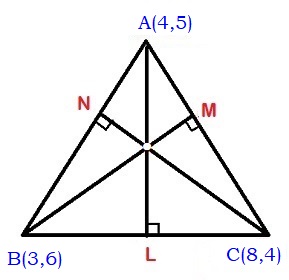
enter image source here

Slope of #bar(AB) =(5-6)/(4-3)=-1/1=-1#

#bar(AB)_|_bar(CN)=>#slope of # bar(CN)=1# ,

# bar(CN)# passes through #C(8,4)#

#:.#The equn. of #bar(CN)# is #:y-4=1(x-8)#

#=>y-4=x-8#

#=>y=x-8+4#

#i.e. color(red)(y=x-4.....to (1)#

Now, Slope of #bar(AB) =-1# and #bar(AB)# passes through
#A(4,5)#

So, eqn. of #bar(AB)# is: #y-5=-1(x-4)#

#=>y-5=-x+4#

#=>color(red)(y=9-x...to(2)#

from #(1)and (2)#

#x-4=9-x#

#=>x+x=9+4=>2x=13=>color(blue)(x=13/2=6.5#

From #(1) ,#

#y=13/2-4=>color(blue)(x=5/2=2.5#

#=>N(13/2,5/2) and C(8,4)# are the endpoints of altitudes
going through corner #C#

Using Distance formula,

#CN=sqrt((13/2-8)^2+(5/2-4)^2)=sqrt(9/4+9/4)#
#:.CN=sqrt(18/4)=sqrt(9/2)#

#:.CN=3/sqrt2~~2.12#