Analyzing Polar Equations for Conic Sections

Key Questions

• How do I find the directrix and focus of a parabola?

  There are two basic kinds of parabola(as it is convenient for me to say)

  Type 1:
  The parabola lying on, or parallel to the #x-#axis

  This parabola is of the form #(y-y_v)^2=4a(x-x_v)#

  Where,
  - focus is #(a+x_v,y_v)#
  - directrix is the line #x=x_v-a#
  - Vertex is #(x_v,y_v)#

  Type 2:
  The parabola lying on, or parallel to the #y-#axis

  This parabola is of the form #(x-x_v)^2=4a(y-y_v)#

  Where,
  - focus is #(x_v,a+y_v)#
  - directrix is the line #y=y_v-a#
  - Vertex is #(x_v,y_v)#

  Antoine · 1 · Apr 18 2015
• How do I find the directrix of a hyperbola?

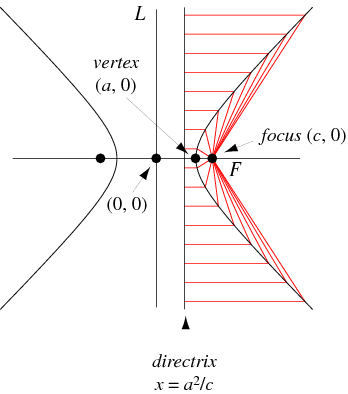
  Answer:

  The directrix is the vertical line #x=(a^2)/c#.

  Explanation:

  For a hyperbola #(x-h)^2/a^2-(y-k)^2/b^2=1#,

  where #a^2+b^2=c^2#,

  the directrix is the line #x=a^2/c#.

  

  mason m · 14 · Jan 1 2016

• How do I find the directrix and focus of a parabola?
• How do I find the directrix of a hyperbola?
• How do I find the directrix of the parabola whose equation is #y=x^2/32#?
• How do I find the directrix of the parabola #y=2x^2#?
• Where is the vertical directrix of a conic if the denominator of its polar equation has the form #1-e cosq#?
• How do you find the points of intersection of the curves with polar equations #r=6costheta# and #r=2+2costheta#?
• How do you find the eccentricity, directrix, focus and classify the conic section #r=0.8/(1-0.8sintheta)#?
• How do you find the eccentricity, directrix, focus and classify the conic section #r=2/(1+2costheta)#?
• How do you find the eccentricity, directrix, focus and classify the conic section #r=10/(2-2sintheta)#?
• How do you find the eccentricity, directrix, focus and classify the conic section #r=8/(4-1.6sintheta)#?
• How do you find the eccentricity, directrix, focus and classify the conic section #r=14.4/(2-4.8costheta)#?
• How do you name the curve given by the conic #r=6#?
• How do you name the curve given by the conic #r=4/(1+costheta)#?
• How do you name the curve given by the conic #r=4/(1+2sintheta)#?
• How do you name the curve given by the conic #theta=(2pi)/3#?
• How do you name the curve given by the conic #r=6/(2+sintheta)#?