How do the bond angles compare for #"ClO"_2#, #"ClO"_2^(-)#, and #"Cl"_2"O"#? Explain why.
1 Answer
I got a questionable result, based on two sources giving me borderline bond angles.
#stackrel(117.40^@)overbrace("ClO"_2) > stackrel(~~111^@)overbrace("ClO"_2^(-)) > stackrel(110.88^@)overbrace("Cl"_2"O"),#
if the bond angle in
#stackrel(117.40^@)overbrace("ClO"_2) > stackrel(110.88^@)overbrace("Cl"_2"O") > stackrel(~~110^@)overbrace("ClO"_2^(-)),#
if the bond angle in
It's just too close to be sure either way unless your book has more precise bond angles in the answer key.
For reference, the electronegativity of
#"Cl"_2"O"# has oxygen at the center (with chlorine having its typical valency as a halogen), and has#7+7+6 = 20# total valence electrons to distribute. The major resonance structure is:
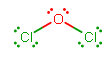
Since oxygen is more electronegative, the negative electron density is mostly concentrated onto oxygen, which is closer to each bonding-electron pair (the electron density is closer together when you look near oxygen).
Therefore, oxygen's share of electron density repels the bonding-electron pairs more easily in each
#"Cl"-"O"# bond than if the electronegativity difference was smaller.This competes with the lone-pair repulsion, which would have contracted the bond angle...
Overall, the competing effects stack to increase the bond angle to a bit more than the expected
#109.5^@# , because...Its actual bond angle is about
#color(blue)(110.88^@)# .
#"ClO"_2# has#7+6+6 = 19# total valence electrons to distribute (yes, it's paramagnetic). The major resonance structure is:
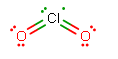
With two double bonds, the bonding-electron pairs repel each other more so than with comparable single bonds, increasing the bond angle above the standard
#109.5^@# .Since
#"O"# atom is larger than#"Cl"# atom, that also contributes to the substantially larger bond angle than in#"Cl"_2"O"# .We also have the one less valence electron on
#"Cl"# than in#"ClO"_2^(-)# , giving less "lone-pair" repulsion, and thus less contraction of the#"O"="Cl"="O"# bond angle by the#"Cl"# valence electrons, relative to one more valence electron on#"Cl"# . This further increases the bond angle.Its actual bond angle is about
#color(blue)(117.40^@)# .
#"ClO"_2^(-)# has#7+6+6+1 = 20# total valence electrons to distribute. The major resonance structure is:
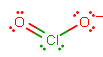
The bond order of each
#"Cl"stackrel(--" ")(_)"O"# bond in the resonance hybrid structure (roughly#1.5# ) is lower than the bond order in each#"Cl"="O"# bond in#"ClO"_2# (pretty much#2# ).Therefore, there is less electron density in each
#"Cl"stackrel(--" ")(_)"O"# bond, allowing the ion's#"O"-"Cl"-"O"# bond angle to contract a little, relative to the same bond angle in#"ClO"_2# .However, the fourth valence electron on
#"Cl"# contracts the bond angle relative to#"ClO"_2# even more than if there were only three nonbonding valence electrons on#"Cl"# . How much smaller of a bond angle we get, I'm not sure.I cannot find a more precise actual bond angle than
#111^@# .However, this source unfortunately lists a poor-precision angle of
#110^@ pm 2^@# , which adds some confusion.
Therefore, the bond angle order is questionable.
#color(blue)(stackrel(117.40^@)overbrace("ClO"_2) > stackrel(~~111^@)overbrace("ClO"_2^(-)) > stackrel(110.88^@)overbrace("Cl"_2"O")),#
if the bond angle in
#color(blue)(stackrel(117.40^@)overbrace("ClO"_2) > stackrel(110.88^@)overbrace("Cl"_2"O") > stackrel(~~110^@)overbrace("ClO"_2^(-))),#
if the bond angle in
It's just too close to be sure either way unless your book has more precise bond angles in the answer key.

