A rectangle #OABC# is drawn so that #O# is the vertex of parabola #y=x^2# and #OA# and #OB# are two chords drawn on the parabola. What is the locus of point #C#?
(A). #y=x^2+2#
(B). #y=-x^2+4#
(C). #y=2x^2#
(D). #y=-2x^2+4#
(A).
(B).
(C).
(D).
2 Answers
(A)
Explanation:
The parabola
As the sides
Now intersection of
As
Below is shown the graph and rectangle relating to
graph{(y-x^2)(2y+x)(y-2x)(8x-4y+5)(2x+4y-20)(y-x^2-2)=0 [-4.84, 5.16, -0.38, 4.62]}
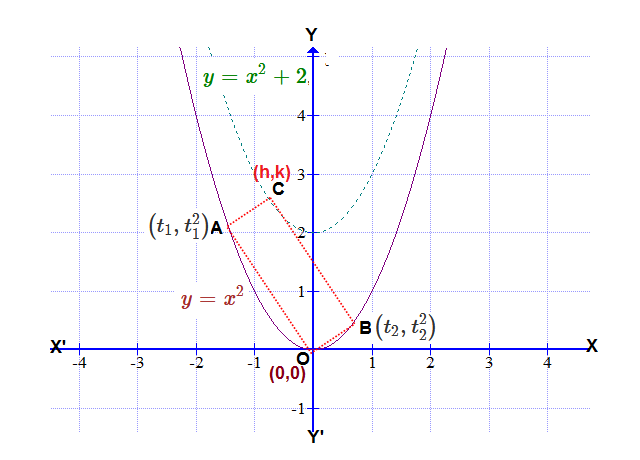
I think that name of the rectangle should be
Let the coordinates of
A
#->(t_1,t_1^2)#
B#->(t_2,t_2^2)#
C#->(h,k)#
O#->(0,0)#
Gradient of OA
Gradient of OB
As OA and OB are adjacent sides of the rectangle then product of their gradients should be
Hence
Now the diagonals ºC and
So coordinates of mid point of
And coordinates of mid point of
Hence
So
Converting

