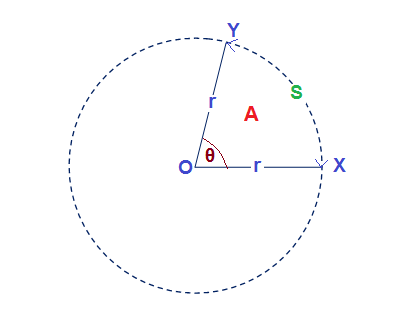
Let us consider a sector of #XOY# of a circle of radius #r# which has been formed by an arc of length #S#. This arc subtends angle #theta # radian at the center #O# of the circle.
Now #S/r=theta#
#=>S=rtheta....[1]#
Let the perimeter of the sector #P=S+2r......[2]#
Combining [1] and [2] we get
#P=rtheta +2#
#=>r=P/(theta+2).....[3]#
Now area of the sector #A=(pir^2)/(2pi)xxtheta#
#=>A=r^2/2xxtheta.....[4]#
Combining [3] and [4] we get
#A=1/2xxP^2/(theta+2)^2xxtheta#
Now
#A=P^2/2xxtheta/(theta^2+4theta+4)#
#=>A=P^2/2xx1/(theta+4+4/theta)#
#=>A=P^2/2xx1/((sqrttheta-2/sqrttheta)^2+8).....[5]#
By the given condition the perimeter #P# of the sector is fixed or constant . So #A# will be maximum when denominator of the RHS of [5] is minimum and this is possible only when
#(sqrttheta-2/sqrttheta)=0#
#=>theta =2# radian
Hence option (D) is correct


