Prove that the largest isosceles triangle that can be drawn in a circle, is an equilateral triangle?
1 Answer
Please see below.
Explanation:
Let their be an isosceles triangle ABC inscribed in a circle as shown, in which equal sides
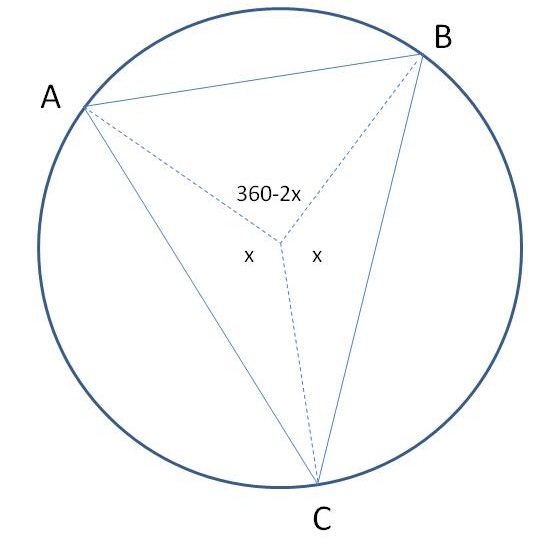
As the area of the triangle portion subtended by an angle
the complete area of triangle ABC is
=
=
=
For maximization we should have
i.e.
or
or
or
or
or
Hence
i.e.
But for a triangle
hence
and hence for maximum area triangle must be equilateral.
