What is the area of a semicircle with radius #8# cm?
1 Answer
Consider a circle of radius
Here's a diagram of what's going on.
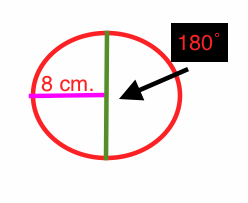
Before applying the formula, let's convert
We will now use the formula to determine the area of this semi-circle.
We can confirm this using the formula for area of a semi-circle,
Same, so both formulae work.
Here are a few problems for you practice.
Practice exercises:
Determine the area of the following semi-circles.
a) The semi-circle contained inside a circle of radius
b) The semi-circle contained inside a circle of diameter
c) The semi-circle contained inside a circle of circumference
Hopefully this helps, and good luck!

