Why perpendicular bisectors of any triangle intercept in the center of circumscribed circle?
1 Answer
Dec 19, 2015
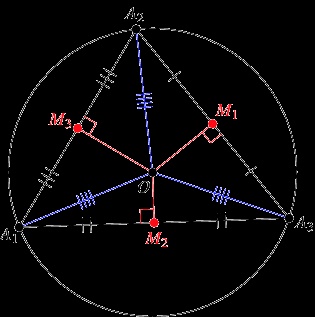
The result follows quickly from the theorem that given a chord of a circle, the perpendicular bisector of that chord passes through the center of the circle.
With this theorem available, we have:
Every side of the triangle is a chord of the circle, and thus passes through the center.
The bisectors, being nonparallel lines, meet at exactly one point.
As each bisector passes through the center, that must be the point at which they meet.
▄
A succinct proof of the theorem used above is given here.

