This figure shows circle O with diameter QS . mRQS=290∘ What is the measure of ∠ROS ?
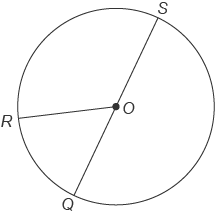
2 Answers
Jun 9, 2017
The situation described seems to be impossible.
Explanation:
The ambiguity in my response is based on the 4 non-displayable characters following "mRQS".
If I ignore these characters so the question claims
then the situation is impossible. If
Jun 10, 2017
Explanation:
As the complete circle is
