Question

Question #04430

Answer 1

The viewing angle between the base and top of the castle wall from the person on the boat will be

`theta=beta-alpha=19.8^@-9.1^@=10.7^@`

Explanation:

Let the angle of elevation of the top of the cliff or base of the castle from the boat be `alpha` and the angle of elevation of the top of the castle from the boat be `beta`

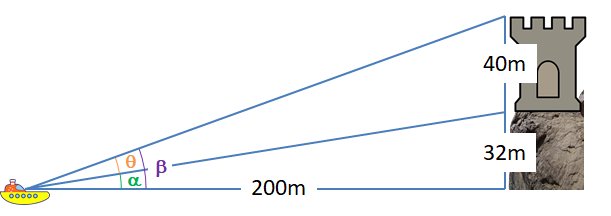
Again the perpendicular distance of the boat from the castle or cliff is `200m`

Height of the top of castle wall is `32m+40m=72m`

Height of the base of castle wall or top of the cliff is `32m`

So `tan beta=72/200=0.36`

`=>beta=tan^-1(0.36)=19.8^@`

And `tan alpha=32/200=0.16`

`=>alpha=tan^-1(0.16)=9.1^@`

Hence the viewing angle between the base and top of the castle wall from the person on the boat will be

`theta=beta-alpha=19.8^@-9.1^@=10.7^@`

Answer 2

`10^@42'31''` or `10.7^@`

Explanation:

Viewing `angle` between bottom of wall and level line to
the foot of the cliff:-`=32/200=tan theta=9^@5'25''`

Vertical height between the foot of the cliff and top of wall

`=40+32=72m`

Viewing `angle` between bottom of cliffl and level line to
the top of the wall:-`=72/200=tan theta=19^@47'56''`

`=`the viewing angle between the base and the top of
the castle wall :-

`(19^@47'56'')-(9^@5'25'')=10^@42'31''` or `10.7^@`