Question

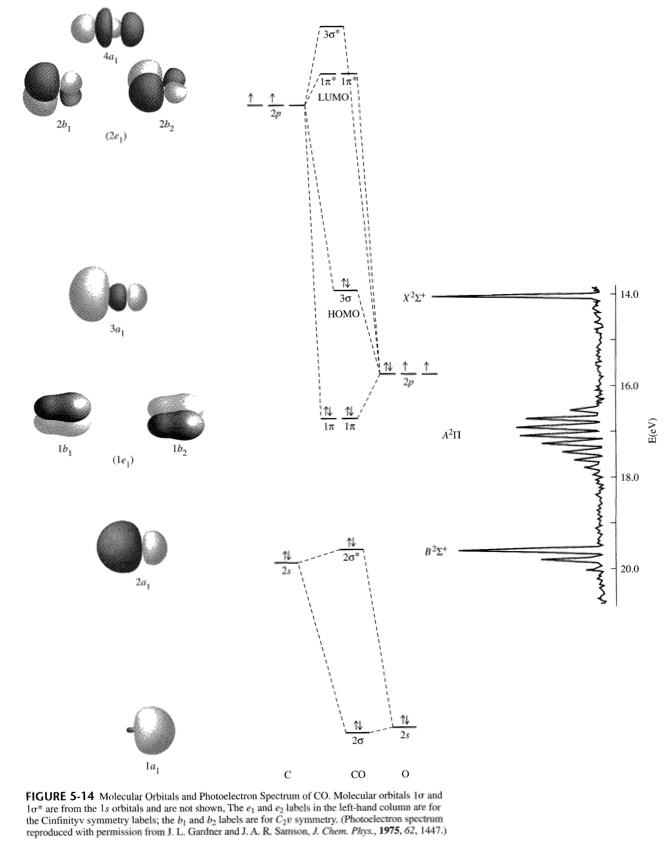
How do I draw the MO diagrams for `"O"_2^-` and `"CO"^(+)` and find out which one is paramagnetic?

Answer 1

Well, the MO diagrams for `"O"_2` and `"CO"` (i.e. both neutral compounds) are below.

• For `ul("O"_2^(-))`, just take the MO diagram of `"O"_2` and add one electron into the `pi_(2px)^"*"` antibonding molecular orbital.
• For `ul("CO"^(+))`, just take out one of the electrons from the `3sigma` HOMO from the MO diagram of `"CO"`.

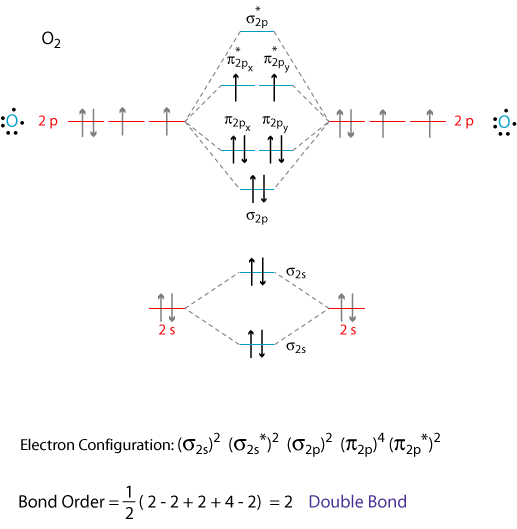
Both substances are paramagnetic, as they have at least one unpaired electron in a given orbital. `"O"_2^(-)` has the unpaired electron in a `pi^"*"` antibonding orbital, and `"CO"^(+)` has the unpaired electron in a `sigma` bonding orbital.

The unpaired electron orients itself in the direction of an applied magnetic field, and gives rise to a total magnetic moment `mu_(S+L) = 2.00023sqrt(S(S+1) + 1/4L(L+1))` in units of `"Bohr Magnetons"`. It is a function of

• the total electron spin `S = |sum_i m_(s,i)|`
• the total orbital angular momentum `L = |sum_i m_(l,i)|`

for the `i`th electron, where `m_l` and `m_s` are the angular momentum and spin quantum numbers, respectively.

The total magnetic moment is a value that can be obtained experimentally from magnetic susceptibility measurements.