Question

Which one is the electron configuration of `"Fe"^(+)`? `[Ar] 3d^5 4s^1`, or `[Ar]3d^6`?

Answer 1

Neither of them are correct! The correct electron configuration is `[Ar] 3d^6 4s^2`...

---

Consider the following diagram...

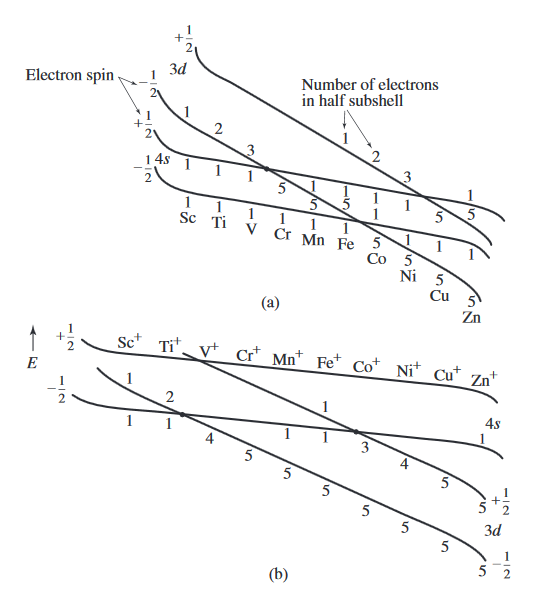
By the convention given in the diagram, the first electron in an orbital is taken to have spin down, `m_s = -1/2`. In `(b)`, note the relative energies of the `3d` electrons and `4s` electron of `color(red)("Fe"^(+))`:

`overbrace(E_(3d(m_s = -1//2)))^("5 electrons") < overbrace(E_(4s(m_s = -1//2)))^"1 electron" < overbrace(E_(3d(m_s = +1//2)))^"1 electron" < overbrace(E_(4s(m_s = +1//2)))^"1 electron"`

This means for `"Fe"^(+)`, so far, the `4s` orbital is such that the first electron in the `4s` orbital (with `m_s = -1//2`) is lower in energy than the sixth `3d` electron.

That establishes the electron configuration `color(red)([Ar]3d^6 4s^1)` for `color(red)("Fe"^(+))`.

In diagram `(a)`, we see `"Fe"` (not `"Fe"^(+)`), decreasing its `4s` orbital energy (the `4s` curves shifted down!), so that...

`overbrace(E_(4s(m_s = -1//2)))^"1 electron" < overbrace(E_(3d(m_s = -1//2)))^("5 electrons") < overbrace(E_(4s(m_s = +1//2)))^"1 electron" < overbrace(E_(3d(m_s = +1//2)))^"1 electron"`

This then agrees with experiment, that the electron configuration of `"Fe"` is...

`color(blue)ul([Ar]3d^6 4s^2)`

Now you may wonder,

"why is the `4s` ionized instead of the `3d` first, even though in `Fe`, the sixth `3d` electron is highest in energy?"

The radial extent of the `4s` is farther out, so its electrons are more accessible for ionization:

The `3d` electrons are also stabilized by a greater effective nuclear charge. That rapid decrease in `Z_(eff)` across the transition metals is shown in the steeper slope of the `3d` curves in the above diagrams `(a)` and `(b)` than for the `4s` curves.

So, the `3d` is not readily ionized.