A building casts a shadow that is 88 meters long. The straight-line distance from the top of the building to the end of the shadow it creates is at a 32° angle with the ground. What is the approximate height of the building?
1 Answer
54.99 meters
Explanation:
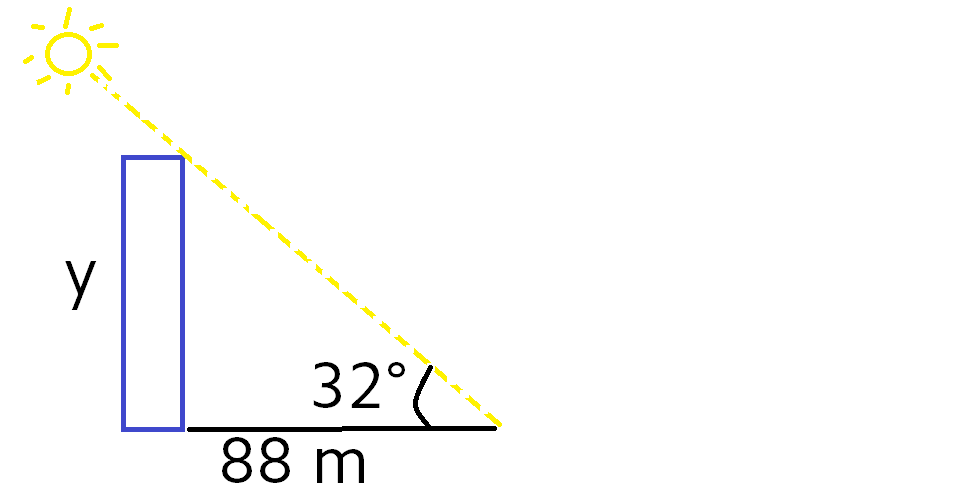
This is a side view image of the building. Every object in the presence of light or emitting light is constantly diverging rays, including the sun. In this example, one of the light rays (dashed yellow line) is perfectly aligned with the building's corners, so it just merely passes over the building, which creates the shadow that's 88 meters long.
This becomes a trigonometry problem because a right angle is formed... We know that
#tan(32°)=y/(88)# .
Now, solve for y to get the height of the building by
Hope this helps!


