Question

A gas occupies 246 mL at 567.3 Torr and 24.0 °C. When the pressure is changed to 771.0 Torr, what temperature is needed to maintain the same volume?

Answer 1

`32.6^@"C"`

Explanation:

It's always a good idea to start with what you know.

You know that the volume of the container, which is given to you as `"246 mL"`, must remain constant. Since no mention of the number of moles of gas was made, you can safely assume that it remains constant as well.

This means that only temperature and pressure will change.

When volume and number of moles are kept constant, pressure and temperature have direct relationship - this is known as Gay Lussac's Law.

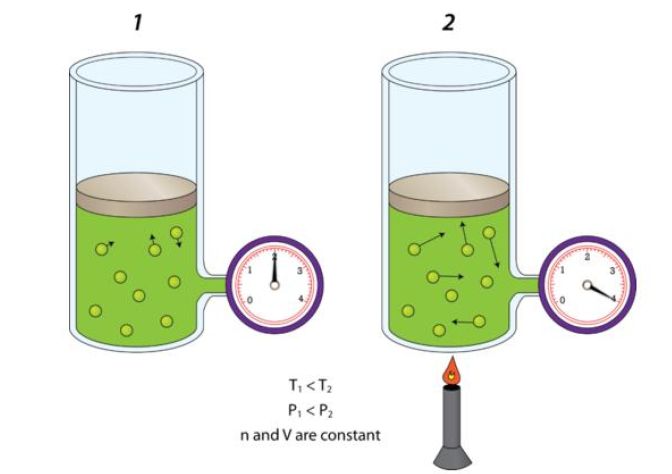
In other words, if pressure increases, temperature increases as well. If pressure decreases, temperature decreases as well.

Mathematically, this is written as

`P_1/T_1 = P_2/T_2" "`, where

`P_1`, `T_1` - the pressure and temperature of the gas at an initial state;
`P_2`, `T_2` - the pressure and temperature of the gas at a final state.

In your case, you know that the pressue is increasing from `"567.3 torr"`, to `"771.0 torr"`. This means that you can expect the needed temperature to be higher than the initial `24.0^@"C"`.

Plug in your values and solve for `T_2`

`T_2 = P_2/P_1 * T_1`

`T_2 = (771.0color(red)(cancel(color(black)("torr"))))/(567.3color(red)(cancel(color(black)("torr")))) * 24.0^@"C" = color(green)(32.6^@"C")`

As predict, the temperature must be higher than what it initially was.